Peter Yu
- 19
- 1
- TL;DR
- Proof of Commutator Operator Identity used in Harmonic Oscillator of Quantum Mechanics
Hi All,
I try to prove the following commutator operator Identity used in Harmonic Oscillator of Quantum Mechanics. In the process, I do not know how to proceed forward. I need help to complete my proof.
Many Thanks.
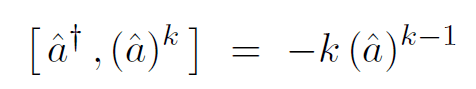
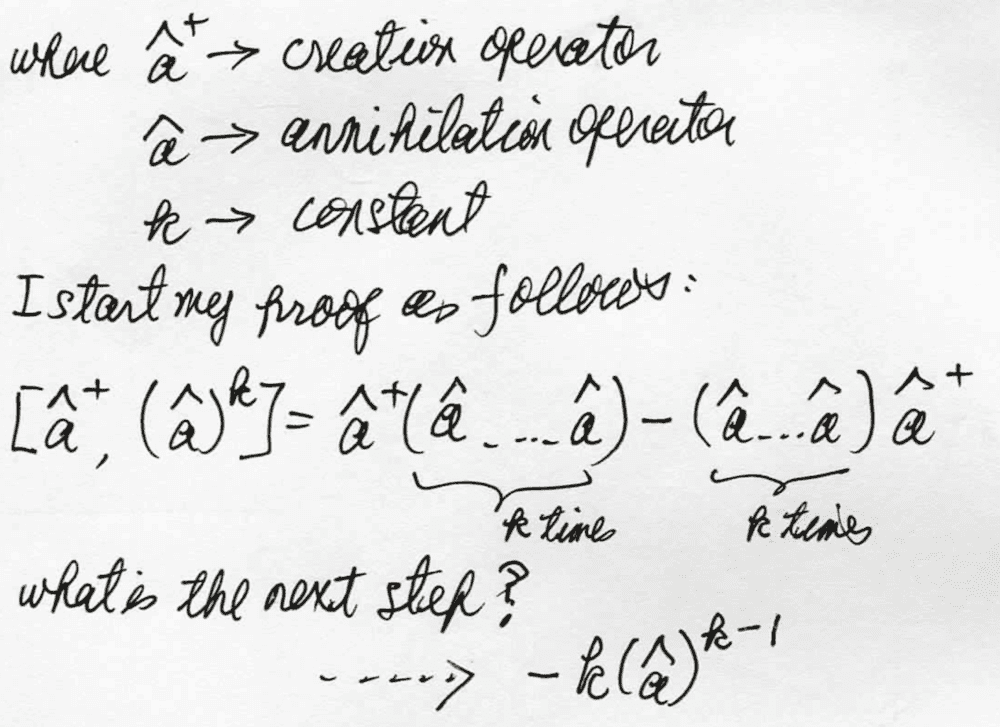
I try to prove the following commutator operator Identity used in Harmonic Oscillator of Quantum Mechanics. In the process, I do not know how to proceed forward. I need help to complete my proof.
Many Thanks.