Proof of cos(θ +ϕ)=cosθ cosϕ - sinθsinϕ via Cartesian Orthogonal Triad

[Angello90]

Homework Statement

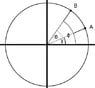
Derive an expression for the scalar product of a and b if the two vectors are written in terms of the usual Cartesian orthogonal triad i, j, k.
By an appropriate choice of a and b, verify the trigonometric identity

cos(θ +ϕ) = cosθ cosϕ − sinθsinϕ

Homework Equations

a.b=|a||b|Cosθ

The Attempt at a Solution

So dot product in Cartesian is:

a=(x1)i + (x2)j + (x3)k
b=(y1)i + (y2)j + (y3)k

(x1)(y1) + (x2)(y2) + (x3)(y3) = ((x1)^2+(x2)^2+(x3)^2)^(1/2)((y1)^2+(y2)^2+(y3)^2)^(1/2)Cosθ

But how can I use this to prove the identity mentioned above?

Please send me some ideas.

Cheers

 

[jeppetrost]

It's a lot easier, if you leave out the third dimension for now.
Try drawing the unit circle and see if you can find some vectors whose |a||b|cos(angle) equals cos(θ +ϕ). Now find the cartesian notation for these two vectors and dot them like you wrote. You should see the result come from thin air about now.

 

[Angello90]

Ok so I draw this (attachment), and I assigned A= 2i+j and B=i+2j

for |a||b|Cosθ I ended up with ((5)^1/2)((5)^1/2)(4/5) = 4

but for the Cos(ϕ+ɣ) I got 3/5

are angles wrong?

 

[jeppetrost]

Euhm, i don't know about the numbers, but try to make it more abstract.
Don't necessarily assign numbers to the vectors, but just symbols.
For instance, if the vector A is ( Cosθ , Sinθ ), then what? What other vector (which is a little like this one) could you use to prove it?

 

[Angello90]

could B be (Cosϕ, Sinϕ)?

 

[jeppetrost]

Since the sizes are 1, |a||b|cos(angle) gives Cos(θ - ϕ) and the usual dot product gives a.b=CosθCosϕ+SinθSinϕ.. since the two are equal, you've showed that Cos(θ - ϕ)=CosθCosϕ+SinθSinϕ. But that's just a minus away from the result. Remember, that sin(-ɣ)=-sin(ɣ) and cos(-ɣ)=cos(ɣ).

 

[Angello90]

Ok thanks for the help. At least now I understand it a little bit better.

Cheers