Proof of Existence of Tensor Product .... Further Question ...

[Math Amateur]

I am reading Bruce N. Coopersteins book: Advanced Linear Algebra (Second Edition) ... ...

I am focused on Section 10.1 Introduction to Tensor Products ... ...

I need help with another aspect of the proof of Theorem 10.1 regarding the existence of a tensor product ... ...The relevant part of Theorem 10.1 reads as follows:

In the above text we read the following:" ... ... Recall that V_1 \times \ ... \ \times V_m = X and that Z is a vector space based on X. Since W is a vector space and f is a map from X to W, by the universal property of Z there exists a unique linear transformation S \ : \ Z \longrightarrow W such that S restricted to X is f. ... ..."Now I have summarised the mappings involved in Theorem 10.1 in Figure 1 below ... ...

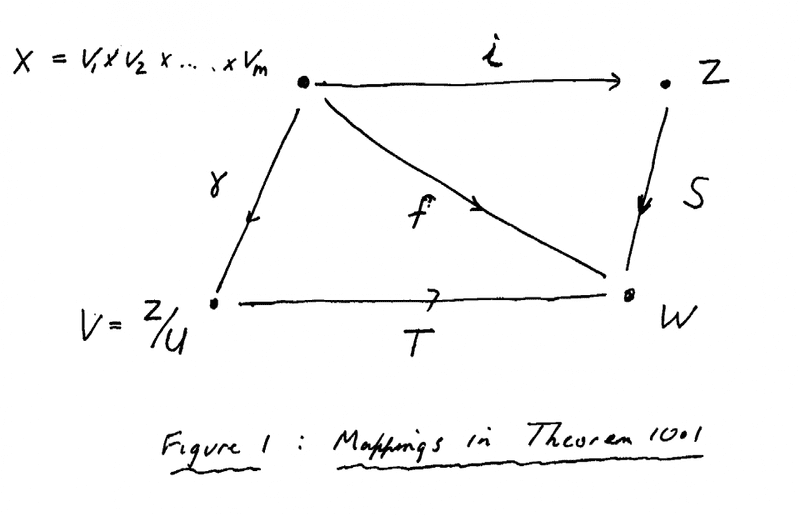My question is as follows:

Why does Z have a universal mapping property ...? ... ... and indeed if Z has one, why doesn't V ... ... giving us the relationship T \gamma = f that we want ... what is special about Z?
Hope someone can help ...

Peter

*** NOTE ***

... ... oh no! ... ... I think I have just realized the answer to my question ... hmm ... embarrassingly simple ... ... I think that Z has a UMP because ( Z, \iota ) is assumed to be the vector space based on the set X... and vector spaces based on a set have a UMP ... is that right? ... see Cooperstein Definition 10.1 on the first page of Section 10.1 provided below ...

Can someone confirm that this is the reason Z has a Universal Mapping Property ...

Peter
==========================================================*** NOTE ***It may help readers of the above post to be able to read Cooperstein's introduction to Section 10.1 where he covers, among other things, the notion of a vector space being based on a set and the idea of the universal mapping problem ... ... so I am providing this text as follows:

 

[WWGD]

I think a helpful thing to know/understand is the concept of maps factoring through (the quotient, here): https://en.wikipedia.org/wiki/List_of_mathematical_jargon in algebra, there are conditions on the kernel of a map. Factoring through is in analogy with the factoring of numbers as products.

You are given functions f:A-->C , g: A-->B . Then f factors through g if there is an h: with f=hg ; h is a map from B-->C. This is I think the clearest way of understanding the tensor product. For vector spaces V,W , the tensor product , $V \ Oline W$ is a vector space in which every bilinear map defined on VxW into a third vector space Z factors through a linear map from the tensor product into Z. The conditions on the kernel guarantee that maps factor through. I will look up the conditions on the kernel and image of the respective groups and get back with it.

 

[Math Amateur]

Thanks WWGD ... most helpful ...

Peter

 

[WWGD]

Thanks WWGD ... most helpful ...

Peter

Glad it helped, Peter, I went through my own pain trying to understand it -- I feel your pain :).

 

[Math Amateur]

Thanks again WWGD ... good to have your support ...

Peter