- #1
slow
- 93
- 16
Hi. Reading some recent threads I have found basic questions about light, fields, etc. For example, why something like light, associated with the electric and magnetic fields, can exist in a vacuum. And I noticed that every time I've been asked that kind of question, I answered "how" the phenomenon behaves and not "why" it happens.
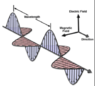
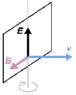
The first thing we learn about light is that it travels in a vacuum in a straight line. We learn it from primary school. Why does light do this ? Then the little book kept in my brain was opened in the chapters of the induction, which operates perpendicularly. But in the case of light in vacuum, ##\vec{E}## and ##\vec{B}## are both transverse, then the mutual perpendicularity is not determining the direction of propagation. Then the little book was opened in Poynting's theorem, which links the power flow in the direction of propagation with ##\vec{E}## and with ##\vec{B}## . But that also does not explain "why" the propagation is rectilinear, since the plane containing ##\vec{E}## and ##\vec{B}## could rotate and the Pointyng vector can do nothing to avoid it .
The barrel of a gun has a helical groove inside. Then the bullet goes spinning and the gyroscopic effect keeps the trajectory straight. If someone asks why the bullet travels rectilinearly in a vacuum, we can give an effective and convincing response. There is a why linked with something proven in the experience. The axis of a gyro maintains the direction while the rotation persists, if nothing intervenes to twist it. We have a "why" in the case of the bullet. It is a physical "why", that is, linked to verifiable experiences.
I need help in the case of light in a vacuum, because I can not find a physical "why", something linked to verifiable experiences.
The first thing we learn about light is that it travels in a vacuum in a straight line. We learn it from primary school. Why does light do this ? Then the little book kept in my brain was opened in the chapters of the induction, which operates perpendicularly. But in the case of light in vacuum, ##\vec{E}## and ##\vec{B}## are both transverse, then the mutual perpendicularity is not determining the direction of propagation. Then the little book was opened in Poynting's theorem, which links the power flow in the direction of propagation with ##\vec{E}## and with ##\vec{B}## . But that also does not explain "why" the propagation is rectilinear, since the plane containing ##\vec{E}## and ##\vec{B}## could rotate and the Pointyng vector can do nothing to avoid it .
The barrel of a gun has a helical groove inside. Then the bullet goes spinning and the gyroscopic effect keeps the trajectory straight. If someone asks why the bullet travels rectilinearly in a vacuum, we can give an effective and convincing response. There is a why linked with something proven in the experience. The axis of a gyro maintains the direction while the rotation persists, if nothing intervenes to twist it. We have a "why" in the case of the bullet. It is a physical "why", that is, linked to verifiable experiences.
I need help in the case of light in a vacuum, because I can not find a physical "why", something linked to verifiable experiences.