Math Amateur
Gold Member
MHB
- 3,920
- 48
I am reading Micheal Searcoid's book: "Elements of Abstract Analysis" ... ...
I am currently focused on understanding Chapter 1: Sets ... and in particular Section 1.4 Ordinals ...
I need some help in fully understanding Theorem 1.4.3 ...
Theorem 1.4.3 reads as follows:
View attachment 8451
View attachment 8452In the above proof by Searcoid we read the following:
"... ... Then $$\beta \subseteq \alpha$$ so that $$\beta$$ is also well ordered by membership. ... ... To conclude that $$\beta$$ is also well ordered by membership, don't we have to show that a subset of an ordinal is well ordered?
Indeed, how would we demonstrate formally and rigorously that $$\beta$$ is also well ordered by membership. ... ... ?
Help will be appreciated ...
Peter
==========================================================================It may help MHB readers of the above post to have access to the start of Searcoid's section on the ordinals ... so I am providing the same ... as follows:
View attachment 8453
It may also help MHB readers to have access to Searcoid's definition of a well order ... so I am providing the text of Searcoid's Definition 1.3.10 ... as follows:
View attachment 8454
View attachment 8455Hope that helps,
Peter
I am currently focused on understanding Chapter 1: Sets ... and in particular Section 1.4 Ordinals ...
I need some help in fully understanding Theorem 1.4.3 ...
Theorem 1.4.3 reads as follows:
View attachment 8451
View attachment 8452In the above proof by Searcoid we read the following:
"... ... Then $$\beta \subseteq \alpha$$ so that $$\beta$$ is also well ordered by membership. ... ... To conclude that $$\beta$$ is also well ordered by membership, don't we have to show that a subset of an ordinal is well ordered?
Indeed, how would we demonstrate formally and rigorously that $$\beta$$ is also well ordered by membership. ... ... ?
Help will be appreciated ...
Peter
==========================================================================It may help MHB readers of the above post to have access to the start of Searcoid's section on the ordinals ... so I am providing the same ... as follows:
View attachment 8453
It may also help MHB readers to have access to Searcoid's definition of a well order ... so I am providing the text of Searcoid's Definition 1.3.10 ... as follows:
View attachment 8454
View attachment 8455Hope that helps,
Peter
Attachments
-
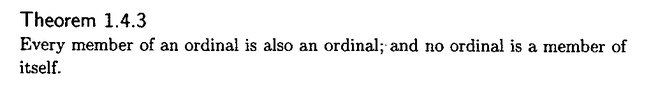 Searcoid - 1 - Theorem 1.4.3 ... ... PART 1 ... .....png1.8 KB · Views: 132
Searcoid - 1 - Theorem 1.4.3 ... ... PART 1 ... .....png1.8 KB · Views: 132 -
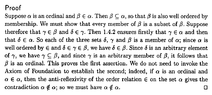 Searcoid - 2 - Theorem 1.4.3 ... ... PART 2 ... ......png13.6 KB · Views: 119
Searcoid - 2 - Theorem 1.4.3 ... ... PART 2 ... ......png13.6 KB · Views: 119 -
 Searcoid - 1 - Start of section on Ordinals ... ... PART 1 ... .....png32.5 KB · Views: 125
Searcoid - 1 - Start of section on Ordinals ... ... PART 1 ... .....png32.5 KB · Views: 125 -
 Searcoid - Definition 1.3.10 ... .....png9 KB · Views: 120
Searcoid - Definition 1.3.10 ... .....png9 KB · Views: 120 -
 Searcoid - 2 - Definition 1.3.10 ... .....PART 2 ... ....png9.1 KB · Views: 116
Searcoid - 2 - Definition 1.3.10 ... .....PART 2 ... ....png9.1 KB · Views: 116
Last edited:
 ope that helps,
ope that helps,