B Prove Bisecting Angle Theorem - 5 Min Exercise

[Qemikal]

Hi, guys, i made an exercise, can you prove this?

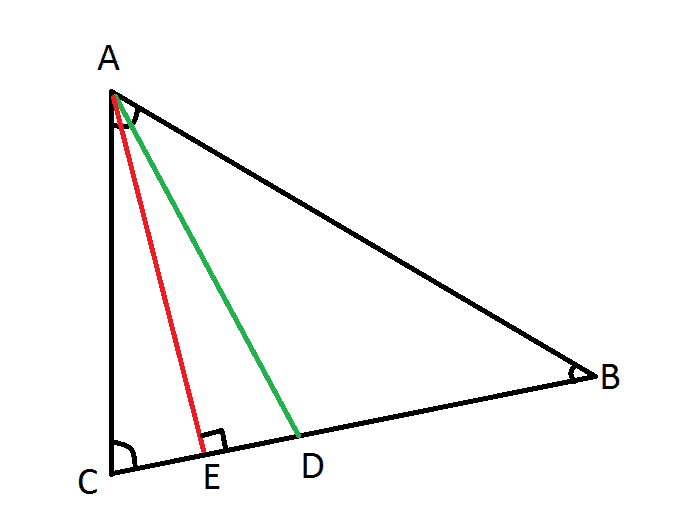
m(∠EAD)=[m(∠ABC)-m(∠ACB)]/2
If you have 5 free minutes, try it, i hope you'll like it!
It's my first own exercise, so I would like some feedback, too.
AD= bisecting(splits angle in 2 equal sides)

 

[HallsofIvy]

You can't prove this, it is, generally, not true. By choosing D at different places along BC, angle EAD can take on many different values while the right side, not depending on D, is fixed. Was there some other condition on D you did not give?

 

[Qemikal]

You can't prove this, it is, generally, not true. By choosing D at different places along BC, angle EAD can take on many different values while the right side, not depending on D, is fixed. Was there some other condition on D you did not give?

My bad, I forgot to add that AD splits the angle in 2 equal sides(angles).

 

[NascentOxygen]

Thread closed for moderation.