anemone
Gold Member
MHB
POTW Director
- 3,851
- 115
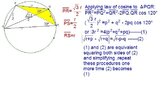
Given a cyclic quadrilateral $PQRS$ where $PQ=p,\,QR=q,\,RS=r$, $\angle PQR=120^{\circ}$ and $\angle PQS=30^{\circ}$.
Prove that $|\sqrt{r+p}-\sqrt{r+q}|=\sqrt{r-p-q}$
Prove that $|\sqrt{r+p}-\sqrt{r+q}|=\sqrt{r-p-q}$