ibnashraf
- 2
- 0
Question:
"Let G be a finite group. Prove that G is a p-group iff every element of G has order a power of p."
this was my attempt at the question:
Suppose G is a p-group
 , where
, where

Let g



Hence, every element of G has order a power of p.
Conversely, suppose that every element of G has order a power of p

But

 divides
divides
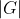
Hence, G is a p-group.can someone look over this and tell me what mistakes i made if any please ?
"Let G be a finite group. Prove that G is a p-group iff every element of G has order a power of p."
this was my attempt at the question:
Suppose G is a p-group
Let g
Hence, every element of G has order a power of p.
Conversely, suppose that every element of G has order a power of p
But
Hence, G is a p-group.can someone look over this and tell me what mistakes i made if any please ?