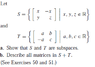Clandry
- 74
- 0
Hi, I was wondering if someone could check my work for this linear algebra problem. I have attached the problem statement in the file "problem" and my work in the file "work." I would type out my work on here, but I couldn't figure out how to put matrices in a post so I just took a pic of my work.
I only attached the work for proving S is a subspace.
I basically checked the 3 conditions my professor gave me to determine if something is a subspace. They are (with respect to my problem):
1. Is the 0 vector in S?
2. If U and V are in S, is U+V in S?
3. If V is in S, then is cV in S for some scalar c?
I feel like I made this problem too complicated. It took me a whole page to just prove S is a subspace.
Can someone verify if that's accurate?
Is there a faster way to do it or a way that takes up less paper?
I only attached the work for proving S is a subspace.
I basically checked the 3 conditions my professor gave me to determine if something is a subspace. They are (with respect to my problem):
1. Is the 0 vector in S?
2. If U and V are in S, is U+V in S?
3. If V is in S, then is cV in S for some scalar c?
I feel like I made this problem too complicated. It took me a whole page to just prove S is a subspace.
Can someone verify if that's accurate?
Is there a faster way to do it or a way that takes up less paper?