Proving Triangle Angles Relation: $\frac{1}{\sin^2 \lambda}$

[anemone]

Inside a triangle $ABC$, there is a point P satisfies $\angle PAB=\angle PBC=\angle PCA=\lambda$. If the angles of the triangle are denoted by $\alpha$, $\beta$ and $\gamma$, prove that

$\dfrac{1}{\sin^2 \lambda}=\dfrac{1}{\sin^2 \alpha}+\dfrac{1}{\sin^2 \beta}+\dfrac{1}{\sin^2 \gamma}$

 

[Albert1]

Inside a triangle $ABC$, there is a point P satisfies $\angle PAB=\angle PBC=\angle PCA=\lambda$. If the angles of the triangle are denoted by $\alpha$, $\beta$ and $\gamma$, prove that

$\dfrac{1}{\sin^2 \lambda}=\dfrac{1}{\sin^2 \alpha}+\dfrac{1}{\sin^2 \beta}+\dfrac{1}{\sin^2 \gamma}$

Spoiler

using the sine law:
View attachment 1935

 

[anemone]

Thanks for participating, Albert!

Solution provided by other:

Spoiler

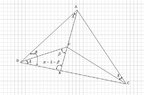
View attachment 1936
First we let AP meet BC at X.

Since $\angle XBP=\angle BAX=\lambda$ and $\angle BXP=\angle AXB=\text{common angle}$, we can say that triangle XPB and XBA are similar. Then we have $\dfrac{XB}{XP}=\dfrac{XA}{XB}$

Applying the sine law to the triangle XBA and considering the fact that $\dfrac{XB}{XP}=\dfrac{XA}{XB}$ give us

$\dfrac{\sin \lambda}{\sin \beta}=\dfrac{XB}{XA}$

$\dfrac{\sin^2 \lambda}{\sin^2 \beta}=\dfrac{XB^2}{XA^2}=\dfrac{XAXP}{XA^2}= \dfrac{XP}{XA}$

Now, the ratio of the area of the triangles XPB to XBA and triangles XCP to XCA are

$\dfrac{\text{area of the triangle XPB}}{\text{area of the triangle XBA}}=\dfrac{XP}{XA}$ and

$\dfrac{\text{area of the triangle XCP}}{\text{area of the triangle XCA}}=\dfrac{XP}{XA}$

This tells us $\dfrac{\text{area of the triangle XPB}}{\text{area of the triangle XBA}}=\dfrac{\text{area of the triangle XCP}}{\text{area of the triangle XCA}}=\dfrac{\text{area of the triangle BPC}}{\text{area of the triangle ABC}}$

$\therefore \dfrac{\sin^2 \lambda}{\sin^2 \beta}=\dfrac{\text{area of the triangle BPC}}{\text{area of the triangle ABC}}$

By the similar arguments, we have

$\therefore \dfrac{\sin^2 \lambda}{\sin^2 \alpha}=\dfrac{\text{area of the triangle APB}}{\text{area of the triangle ABC}}$

$\therefore \dfrac{\sin^2 \lambda}{\sin^2 \gamma}=\dfrac{\text{area of the triangle CPA}}{\text{area of the triangle ABC}}$

Hence,

$\small\dfrac{\sin^2 \lambda}{\sin^2 \alpha}+\dfrac{\sin^2 \lambda}{\sin^2 \beta}+\dfrac{\sin^2 \lambda}{\sin^2 \gamma}=\dfrac{\text{area of the triangle APB}}{\text{area of the triangle ABC}}+\dfrac{\text{area of the triangle BPC}}{\text{area of the triangle ABC}}+\dfrac{\text{area of the triangle CPA}}{\text{area of the triangle ABC}}=1$

$\dfrac{1}{\sin^2 \lambda}=\dfrac{1}{\sin^2 \alpha}+\dfrac{1}{\sin^2 \beta}+\dfrac{1}{\sin^2 \gamma}$ (Q.E.D.)