Riman643
- 62
- 2
- Homework Statement
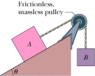
- Body A in the figure weighs 93 N, and body B weighs 57 N. The coefficients of friction between A and the incline are μs = 0.40 and μk = 0.22. Angle θ is 47°. Let the
positive direction of an x axis be up the incline. What is the acceleration of A if A is initially (a) at rest, (b) moving up the incline, and (c) moving down the incline?
- Relevant Equations
- fs = Nμs
fk = Nμk
F = ma
a) I figured this part out. Because A is at rest that means the acceleration is 0
b&c) I am completely lost how to go about this. I drew a free body diagram for A and I was able to determine 4 forces acting on it.
1: The Gravitational force on A (GA). Using the angle (θ), and the incline as my x-axis I was able to determine
GAx = GAsin(θ) = 93sin(47) = 68.02 N
GAy = GAcos(θ) = 93cos(47) = 63.43 N
2: The Normal force on A (NA). This is equal to GAy.
NA = GAy = 63.43 N
3: The static and kinectic frictional forces on A (fsA, fkA). I found these using the static and kinetic friction coefficients (μsA, μkA) and the Normal force.
fsA = NAμsA = 0.40(63.43) = 25.37 N
fkA = NAμkA = 0.22(63.43) = 13.95 N
4: The Tension force on A (TA). It is very tempting to say that it is equal to weight of B, but for the forces to be at rest or for A to move up the ramp TA would have to be much greater.
I really need help in 1) Finding TA and 2) Figuring out how the two frictional forces play a role in this. Since A would already be moving in either direction I feel like I would need to use kinetic friction somehow, but then, what would the point of including static friction in the problem? Any help/tips would be greatly appreciated.
b&c) I am completely lost how to go about this. I drew a free body diagram for A and I was able to determine 4 forces acting on it.
1: The Gravitational force on A (GA). Using the angle (θ), and the incline as my x-axis I was able to determine
GAx = GAsin(θ) = 93sin(47) = 68.02 N
GAy = GAcos(θ) = 93cos(47) = 63.43 N
2: The Normal force on A (NA). This is equal to GAy.
NA = GAy = 63.43 N
3: The static and kinectic frictional forces on A (fsA, fkA). I found these using the static and kinetic friction coefficients (μsA, μkA) and the Normal force.
fsA = NAμsA = 0.40(63.43) = 25.37 N
fkA = NAμkA = 0.22(63.43) = 13.95 N
4: The Tension force on A (TA). It is very tempting to say that it is equal to weight of B, but for the forces to be at rest or for A to move up the ramp TA would have to be much greater.
I really need help in 1) Finding TA and 2) Figuring out how the two frictional forces play a role in this. Since A would already be moving in either direction I feel like I would need to use kinetic friction somehow, but then, what would the point of including static friction in the problem? Any help/tips would be greatly appreciated.