Pulley problem involves Friction static and Kinetic problem

[Leocardinal]

Homework Statement

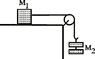
M1 has a mass of 6.51 kg. It is on a horizontal surface, connected by a light string to a hook. Mass M2 can be increased smoothly by adding masses little at a time. The pulley has a negligible mass and no friction.

When M2 is 3.12 kg it begins to accelerate downwards at a rate of 1.52 m/s2. Calculate mu static -mu kinetic for M1 on the surface.

I was also given this hint, First calculate ms (from knowing the force it takes to begin moving) and then mk (from the given acceleration) and subtract

Homework Equations

F= Ma


Mass2
Fnety = T-Mg


Mass1

Fnetx= T-Fstatic

Fs= Mus*Fn

Fk= Muk* FN

The Attempt at a Solution

Mass2
Fnety = T-Mg
-4.74N= T-30.576N
T= 25.83

Mass1

Fnetx= T-Fkinetic
9.89N= 25.83-15.934
Fk= Muk*Fn
15.9348/63.798= 25.83

Muk= .24976

Fnet=0
T-Fs=
25.83

Fs= Mus* FN

25.836= Mus * FN
25.836/63.798

Mus=.405

Mus-Muk= .155

 

[Delphi51]

There is something odd about this solution and I can't quite pin it down. I think you are supposed to write F = ma for each mass as your starting point. This would give you 2 equations:
[1] T - u*m1*g = m1*a and [2] m2*g - T = m2*a
where T is the tension in the string between the two masses.
When a = 0, you get T = u*m1*g from [1] and when you put it into [2] you have m2*g = u*m1*g which gives u = m2/m1 = 0.479 for the static coefficient.