Pulleys - Relationship between mass and aceleration

[AlonsoDeMaria]

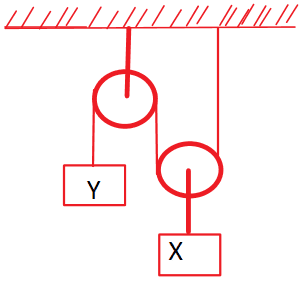
1. Homework Statement

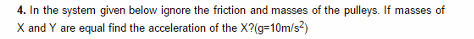
2. Homework Equations
How to get a_x=2a_y?

3. The Attempt at a Solution
a=10m/s²

And the solution I found was a=2m/s²

I found this at : http://www.physicstutorials.org/home/exams/dynamics-exams/142-dynamics-exam1

 

[DEvens]

So, I see you pointing at an exam solution. I don't see your attempt.

The solution you pointed at has a typo. And the explanation for it is wonky. You get the ratio of acceleration of the two masses by conserving string. That is, the string does not change length.

 

[AlonsoDeMaria]

Oh, I am sorry. I didn't want to write all my attempt.

This was my full attempt
I used linear equations to solve this part:
Following the exam solution:
2T-10m=m*a_x
T-10m=m*a_y (I multiplied this by 2) and got 2T-20m=2m*a_y

Then I tried to make a comparison between the accelerations, so I deleted "T" subtracting the first and second equations:
2T-10m - (2T-20m)=m*a_x-2m*a_y
10m=m(a_x-2a_y)

Then 10=(a_x-2a_y). Then, a_y=(10-a_x)/2
I replaced a_y on the second equation:
T-10m=m*(10-a_x)/2
Then, 2T-20m=10m - m*a_x
2T-30m= - m*a_x
-2T+30m= m*a_x
Then I took the first equation and replaced m*a
2T-10m = -2T + 30m
4t=40m , T=10m

And then
20m-10m=m*a_x, 10m=m*a_x, a_x=10m/s²

I need to how to get that a_x=2a_y
And if my answer was correct.

 

[DEvens]

Did you read to the bottom of my post? You get the ratio of accelerations by noting that the length of string does not change. Suppose that the mass X moves up by 1 unit. How far down will Y move?

 

[AlonsoDeMaria]

2 units.

I am checking all again.

 

[AlonsoDeMaria]

So I was reading that a_y= - 2 a^x.
And the answer is 2m/s²

What did I do wrong on my process?

 

[AlonsoDeMaria]

10m=m(ax-2ay)

Then 10=(ax-2ay). Then, ay=(10-ax)/2

So the correct was to write: ay=(ax-10)/2
Even so, using that leads to nowhere.

So the only possibility to solve that was just knowing "conserving string" law.

Is there any other way to solve that without that law?
(Or better for me to create another thread?)

Thank you very much for your help.