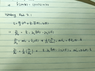Homework Help Overview
The discussion revolves around deriving the equation of motion from a defined Lagrangian in the context of quantum mechanics, specifically referencing Weinberg's Problem 9.1. Participants are engaged in exploring the relationships between the Lagrangian, the equations of motion, and the implications of dimensionality on the definitions used.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning, Assumption checking
Approaches and Questions Raised
- Participants discuss the derivation of the equation of motion and express uncertainty regarding the terms involved, particularly the role of the function f(x). There are attempts to clarify the use of partial derivatives and the implications of dimensionality on the definitions of curl.
Discussion Status
The discussion is ongoing, with participants providing insights and corrections regarding the notation and mathematical expressions. Some guidance has been offered on the proper treatment of variables, but there is no explicit consensus on the clarity of the equations or the next steps in the problem-solving process.
Contextual Notes
Participants note the potential ambiguity in the dimensionality of the coordinates and the definitions of curl in higher dimensions, which may affect the interpretation of the problem. There is also mention of the need for a clearer problem statement for subsequent questions related to the Hamiltonian and Schrödinger equation.