Quantum physics - the wave properties of particles - HELP

[Yael]

hey everyone,
i have a question I'm trying to solve here for class
any help would be SO apreciated !

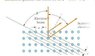
"In the Davisson-Germer experiment, 54.0-eV electrons were diffracted from a nickel lattice. if the first maximum in the diffraction pattern was observed at 50 degrees (as in the figure).
what was the lattice spacing a between the vertical rows of atoms in the figure? (it is not the same as the spacing between the horizontal rows of atoms)"

 

[Chi Meson]

Use the given kinetic energy of the electrons, along with the mass of electrons, to find the momentum. Then ask deBroglie about the wavelength.

 

[Yael]

hmmm Can you just explain how do i use the kinetic Energy (54.0-ev) to find the momentum ?

and once i do find the momentum - De Broglie is for the wavelength. the question is for finding the "a" spacing in the figure...
what about the given angle?

Thanks !

 

[Hootenanny]

Use kinetic energy to find the velocity of the electrons. Then use this velocity to find the momentum. You can then find the DeBroglie wavelength. You need the wavelegth to calculate the spacings. I think you can use the formula for young's double slit.

 

[Yael]

when using the kinetic energy to find V... do i use the expression for relativistic kinetic energy where v/c approaches 1? or do i simply use the classical expression of 1/2 mv squared?
i know this is basic but... :-S

thanks !

 

[Yael]

on the same subject - the expression for diffraction is :
2dsinTheta = m times lamda.
where d is the spacing between the horizontal lines and not the vertical ones :-/
how do i get to "a" ?

 

[Hootenanny]

I've just had a quick glance through any examples of electron scattering I have and none of them take into account relativistic effects. As for calculating 'a', I don't know how you could do it, you will probably have to calculate d then work it out from there. I'll ask the other homework helpers to have a look at it.

 

[gulsen]

What I see from the picture is a \cos(\theta) = d.
As for wavelength, relativistically:
\lambda = \frac{h}{p} = \frac{h}{\sqrt{E^2- (mc^2)^2}/c}
where E = K + mc^2

 

[Doc Al]

on the same subject - the expression for diffraction is :
2dsinTheta = m times lamda.
where d is the spacing between the horizontal lines and not the vertical ones :-/
how do i get to "a" ?

The first thing to do is understand Bragg's law, which is what that equation describes. That will allow you to figure out the separation (d) between the lattice planes and how that relates to the labeled distance (a).

Look here: http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/bragg.html

The Davison-Germer experiment is also discussed here: http://hyperphysics.phy-astr.gsu.edu/hbase/davger.html#c1

 

[Chi Meson]

What I see from the picture is a \cos(\theta) = d.
As for wavelength, relativistically:
\lambda = \frac{h}{p} = \frac{h}{\sqrt{E^2- (mc^2)^2}/c}
where E = K + mc^2

Please correct me if I am wrong, but is a 54 eV electron going fast enough for relativistic analysis?

 

[Hootenanny]

I've just had a quick glance through any examples of electron scattering I have and none of them take into account relativistic effects.

I wouldn't imagine that 54 eV is enough to take into account relativistic effects either. By my reconing the electron would be traveling at 4.37\times 10^6 m\cdot s^{-1}, which is only about 1.46% of the speed of light...

 

[Chi Meson]

That's a gamma of 1.0001, so you can ignore reletivistic effects for this one. So momentum = SQRT(2Km)

 

[Yael]

From what I've understood so far :
a = d sin θ (?)

Thanks for all the help so far everyone.

 

[Hootenanny]

From what I've understood so far :
a = d sin θ (?)

Thanks for all the help so far everyone.

Where did you get that from?

 

[Yael]

oh i was looking at the link that Doc Al posted : http://hyperphysics.phy-astr.gsu.edu...davger.html#c1

to be honest I'm all mixed up with how to get to the "a" :-S
i can't seem to get how gulson got: a cos θ = d

 

[Hootenanny]

I can see how he got a\cos\theta = d, but I'm not sure it's right. You can make a right angled triangle with a being the base and d being the hyp. I'm not sure if this is the correct method. It's probably best to wait until someone with more knowledge comes online.

 

[Doc Al]

to be honest I'm all mixed up with how to get to the "a" :-S
i can't seem to get how gulson got: a cos θ = d

The angle between the normal to the scattering plane (along which "d" is measured) and the horizontal plane (along which "a" is measured) is given by \theta. "a" is the hypotenuse of a right triangle, with "d" as the side adjacent to that angle. Thus d = a \cos\theta.

 

[Yael]

so...
1. at first stage i use the classic expression of kinetic energy (½ mv²) with the 54 ev electron to find the velocity
2. after i obtain V i turn to de broglie to find the wavelength.
3. with the wavelength - i use bragg's law (2dsinθ = mλ) to get to 'd'.
4. use d to get 'a' through: d = a cosθ

hmmm sounds good?

 

[Yael]

getting into atomic physics I'm trying to answer this question but can't seem to understand exactly what they mean by it :
"Does the light emitted by a neon sign constitute a continuous spectrum or only a few colors? Defend your answer"

 

[Hootenanny]

so...
1. at first stage i use the classic expression of kinetic energy (½ mv²) with the 54 ev electron to find the velocity
2. after i obtain V i turn to de broglie to find the wavelength.
3. with the wavelength - i use bragg's law (2dsinθ = mλ) to get to 'd'.
4. use d to get 'a' through: d = a cosθ

hmmm sounds good?

You've got it

"Does the light emitted by a neon sign constitute a continuous spectrum or only a few colors? Defend your answer"

I think another way of looking at it is, "Does a neon sign emitt all wavelengths of visibil light, or does it only emitt a few different wavelengths?" That's my take on it anyway.

 

[Yael]

Got it !

Thanks very Much Hootenanny :-)

 

[gulsen]

Please correct me if I am wrong, but is a 54 eV electron going fast enough for relativistic analysis?

Well, I couldn't remember how big was rest-energy of electron, and wrote the relativistic one just to be safe ^-^'

 

[Yael]

i have another question :-/ i solved it but not too sure.
"A hydrogen atom is in its fifth excited state, with principal quantum 6. The atom emits a photon with a wavelength of 1090 nm. Determine the maximum possible orbital angular momentum of the electron after emission."

so i basically used Balmer's series:
1/λ = RH ( 1/ni – 1/nf²) (RH = Rydberg Constant).
solved for n... got n = 3 and then 'l' can be either 0,1 or 2.
makes sense ? :-/

 

[JoShmoe]

Similar Question

Hey All,
This is actually my first post so I'll try to make it brief :).
I have a similar HW question where I'm supposed to find the v/c for a proton accelerated to 10TeV. I have tried to solve the problem two different ways, each of them giving me the same answer (partly due to round off error on my calculator I'm sure).
I have tried E = mc^2 + .5mv^2 and E = .5mv^2. Both of these gave me v ~ 4.38x10^10 m/s and v/c = 146 m/s. My velocity can't be greater than c so what's going on?
I think part of the problem is related to another HW question that asks for an expession for E = mc^2 expressed as E = rest energy + kinetic energy + first order relativistic correction So far I have: E = mc^2 + .5mv^2
I don't have a clue as to what a first order relativistic correction would be but I suspect if I added it in it would help with the problem.
Any help would be greatly appreciated :-)
~Jo

 

[Hootenanny]

Welcome to PF Jo,

Try using the formula for relativistic Kinetic Energy;

E_{k} = \frac{m_{0}c^2}{\sqrt{1 - \frac{v^2}{c^2}}} - m_{0}c^2

Next time I would recommened that you start a new thread for any new questions you may have.

Regards,
~Hoot

 

[JoShmoe]

Hi Hootenanny,
I appreciate the response. I have done a bit more research and I have even found a couple of simplified and solved problems online [see http://www.antonine-education.co.uk/physics_a2/options/Module_8/Topic_6/TOPIC_6.HTM @ bottom of page] but when I go to solve my problem I still get a velocity greater than c.
My calculations are as follows:
E = mc^2+10TeV
E = mc^2/((1-v^2/c^2)^-.5)
Setting the two equations equal to each other I get v^2 = 1.0000094c^2 --> v = ~ 3.0000141x10^8
I have pretty good round off error because I am using a computer program which is capable of going out past the usual 8 sig-figs of a calculator.
I'm kind of getting annoyed that this problem is turning out to be such a pain when I know that I'm probably just doing something stupid.
Thanks again,
~Jo

 

[Hootenanny]

You don't need to use two equations the only equation you need to use its the one I quoted above.

E_{k} = \frac{m_{0}c^2}{\sqrt{1 - \frac{v^2}{c^2}}} - m_{0}c^2

Put this equal to the amount of energy (10TeV) then solve for \frac{v}{c}. Rememeber to convert eV to J before you start.

Regards,
~Hoot

 

[JoShmoe]

Thanks Hootenanny, I think I have the correct answer now.
Have a good one.
~Jo