DavidAp
- 44
- 0
The double integral xcosy is bounded by y=0, y=x^2, and x=1. I was able to integrate almost wholly through; however, toward the end I was unsure what to do when i was asked to plug in x^2 into x^2. What do I do?!
Here is an image of my work on the white board. Please, if my hand writing is illegible tell me and I would be more than happy to type it all out for you.
Thank you for taking the time to review my question.
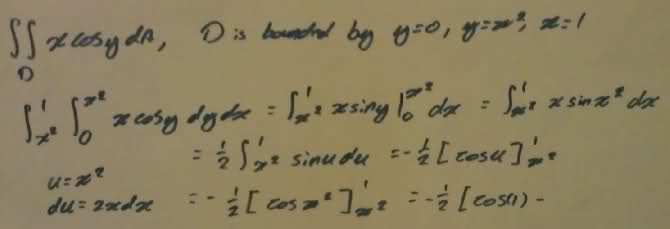
Here is an image of my work on the white board. Please, if my hand writing is illegible tell me and I would be more than happy to type it all out for you.
Thank you for taking the time to review my question.
Last edited: