ScienceGeek24
- 164
- 0
Homework Statement
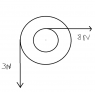
A solid cylinder is pivoted about a frictionless axle as shown. A rope wrapped around the outer radius of 2 m exerts a downward force of 3N. A rope wrapped around the inner radius of 0.7 m exerts a force of 8 N to the right. The moment of inertia of the cylinder is 8 kg m^2. Find the angular acceleration.
Homework Equations
Don't even know whre to start of since i never had a problem like this in mastering physics hm. (this is from a review sheet of my physics test on Tuesday)
The Attempt at a Solution
No idea, I'm in hopes you can orientate me in this one.