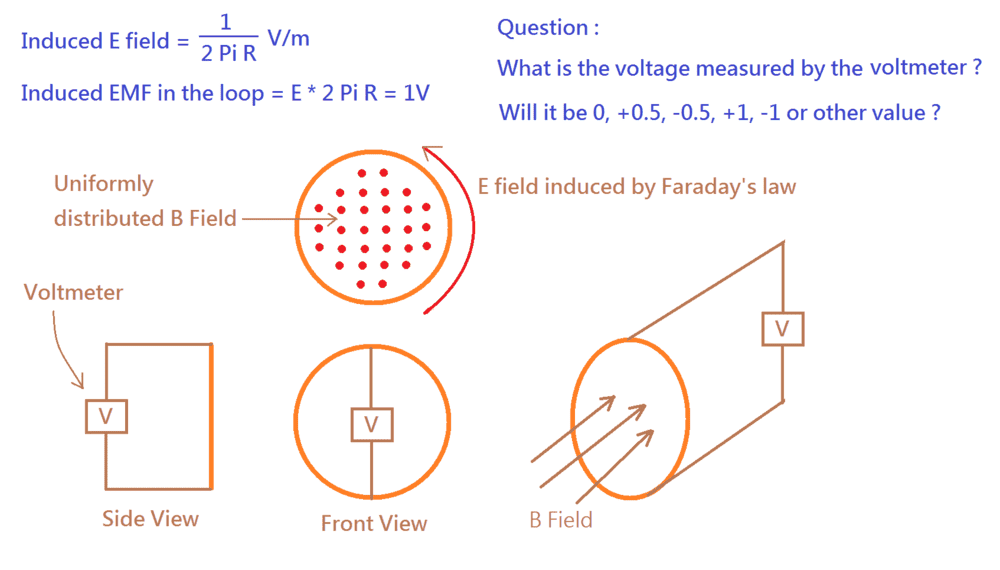
I would like to express my views on the issue of non-conservative electric fields and potential differences.
Although the induced electric field is non-conservative, but for the fixed path and direction in the electric field, such as R1 and R2 shown in the figure below, there can indeed be a potential difference, because their voltage will respectively vary with their resistance, and they consume energy. But, of course, the placement and direction of the two voltmeters and their leads may affect the measured value.
View attachment 272957
Consider again the transformer shown in the figure, the secondary output voltage is also produced by the non-conservative electric field induced by changing magnetic field, therefore, its corresponding line integral of the electric field should only be along the path of the secondary coiled wire. If the line integral follows other paths, of course there may be different results.
In addition, We can see that the placement and direction of the secondary external output circuit loop has no (or extremely little) impact on the output voltage. The reason is obvious, because for the same magnetic flux , it only has one turn, but the number of turns inside the transformer is usually much larger than one turn.