mabdeljaber
- 3
- 3
- Homework Statement
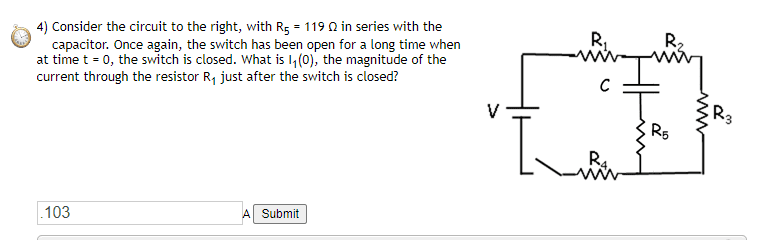
- Consider the circuit to the right, with R5 = 119 Ω in series with the capacitor. Once again, the switch has been open for a long time when at time t = 0, the switch is closed. What is I1(0), the magnitude of the current through the resistor R1 just after the switch is closed?
- Relevant Equations
- I=V/R , Req=R235+R14
So what I know is that without the edition of the R5 resistor R2 and R3 are 0 because the capacitor is short circuiting them. Why does the addition of the R5 resistor cause R2 and R3 to be calculated into the Req for the current equation?
Last edited by a moderator: