SUMMARY
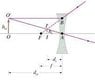
The discussion focuses on calculating image distance and magnification for a concave lens using the lens equation, specifically for an object placed 24 cm in front of a concave lens with a focal length of 18 cm. Participants clarify the sign conventions for object distance (u), image distance (v), and focal length (f), emphasizing that for a concave lens, the focal length is negative. The final calculations yield an image distance of -72 cm and a magnification of +3, indicating that the image is virtual and three times larger than the object.
PREREQUISITES
- Understanding of the lens equation: 1/f = 1/u + 1/v
- Knowledge of sign conventions for lenses and mirrors
- Familiarity with ray diagrams for optical systems
- Basic concepts of virtual and real images
NEXT STEPS
- Study the application of the lens equation in different optical systems
- Learn about ray diagram construction for both concave and convex lenses
- Explore the concept of magnification and its calculation in various scenarios
- Investigate the differences between real and virtual images in optics
USEFUL FOR
Students studying optics, physics educators, and anyone interested in understanding lens behavior and image formation.