BWV
- 1,581
- 1,933
- TL;DR Summary
- Question on problem 7 on July Challenge
Trying to follow and learn from the solution and did not want to clutter up the original thread
My naive question is why doesn't Jensen's Inequality prevent this step?
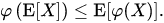
Where you are swapping the expectation of a function for applying the function to the expectation which according to the inequality, the two expressions are equal only if the function is linear, which W^2 is not
nuuskur said:Fubini allows us to change order of integration, so we get
<br /> \mathbb EX = \mathbb E \left ( \int _0^t W_s^2ds\right ) = \int _0^t \mathbb E(W_s^2)ds = \int_0^t sds = \frac{t^2}{2}<br />
My naive question is why doesn't Jensen's Inequality prevent this step?
Where you are swapping the expectation of a function for applying the function to the expectation which according to the inequality, the two expressions are equal only if the function is linear, which W^2 is not