- #1
- 19,659
- 25,639
Questions
1. (solved by @Flatlanderr , solved by @lriuui0x0 ) Show that ##\frac{\pi}{4} + \frac{3}{25} \lt \arctan \frac{4}{3} \lt \frac{\pi}{4} + \frac{1}{6}##
2. (solved by @nuuskur ) Show that the equation ##x + x^3 + x^5 + x^7 = {c_1}^2 (c_1 - x) + {c_2}^2 (c_2 - x)## where ##c_1, c_2 \in \mathbb{R}##, has only one real root.
3. (solved by @KnotTheorist ) Let ##A = \begin{bmatrix}
7 & 3\\
3 & -1
\end{bmatrix}##. Find an orthogonal matrix ##P## such that ##D = P^{-1} A P## is diagonal.
4. (solved by @nuuskur ) Using Calculus, show that the roots of the equation ##x^5 + ax^4 + bx^3 + cx^2 + dx + e = 0## cannot be all real if ##2a^2 \lt 5b##
5. Consider the projective space ##P^m(F_q) = P(F_q^{m+1})##. How many (t+1)-dimensional spaces in this projective space contain a given t-dimensional space?
6. (solved by @nuuskur ) Let ##C## be a subspace of ##F_q^n##. We call ##C## cyclic if ##C## contains its right shifts, i.e. ##x = (c_1, \dots, c_n) \in C \implies \vec{x} = (c_n, c_1 \dots, c_{n-1}) \in C##. Show that there is a correspondence between the cyclic subspaces of ##F_q^n## and the ideals of the quotient ring ##F_q[X]/(X^n-1)##.
7. (solved by @nuuskur ) Let ##(W_t)_{t\geq 0}## be a Brownian motion on a suitable probability space. Put ##X:= \int_{0}^t W_s^2 ds##. Calculate ##E(X).## (changed, 7/5/19)
8. (solved by @nuuskur ) Calculate the Galois group of the splitting field of ##x^4 - 2x^2 -2## over ##\mathbb{Q}##. Determine the isomorph type of the Galois group.
9. Prove that every symmetric and positive definite matrix ##A\in \mathbb{M}(n,\mathbb{R})## can be uniquely written as ##A=L\cdot L^\tau##, where ##L## is a lower triangular matrix with positive diagonal elements.
Calculate ##L## for ##A=\begin{bmatrix}4 &2& 4& 4\\
2& 10& 17& 11\\
4& 17& 33& 29\\
4& 11& 29& 39\end{bmatrix}##.
10. (solved by @nuuskur ) Let ##L\subseteq H## be a nonempty, closed, and convex set in a Hilbert space. Prove that there is an element of minimal norm in ##L##.

11. (solved by @Physics lover ) Solve the following integral
$$I = \int_0^{\pi/2} \frac{\sin^{2019} x}{\cos^{2019} x + \sin^{2019} x}dx$$
12. (solved by @Pi-is-3 ) Is ##N:=21^{39}+39^{21}## divisible by ##45##? Why, why not?
13. (solved by @Pi-is-3 ) Let ##0<u,v,w<1##. Show that among the numbers ##u(1-v)\, , \,v(1-w)\, , \,w(1-u)## is at least one value not greater than ##\dfrac{1}{4}\,.##
14. (solved by @JosephFG ) What is the ratio between the red and the blue area where ##P## and ##Q## are one fifth away from the vertices?
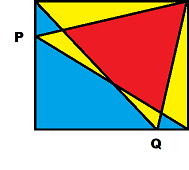
15. (solved by @Pi-is-3 ) In what ratio does the circumference of the circle divide the left and right sides of the square?

1. (solved by @Flatlanderr , solved by @lriuui0x0 ) Show that ##\frac{\pi}{4} + \frac{3}{25} \lt \arctan \frac{4}{3} \lt \frac{\pi}{4} + \frac{1}{6}##
2. (solved by @nuuskur ) Show that the equation ##x + x^3 + x^5 + x^7 = {c_1}^2 (c_1 - x) + {c_2}^2 (c_2 - x)## where ##c_1, c_2 \in \mathbb{R}##, has only one real root.
3. (solved by @KnotTheorist ) Let ##A = \begin{bmatrix}
7 & 3\\
3 & -1
\end{bmatrix}##. Find an orthogonal matrix ##P## such that ##D = P^{-1} A P## is diagonal.
4. (solved by @nuuskur ) Using Calculus, show that the roots of the equation ##x^5 + ax^4 + bx^3 + cx^2 + dx + e = 0## cannot be all real if ##2a^2 \lt 5b##
5. Consider the projective space ##P^m(F_q) = P(F_q^{m+1})##. How many (t+1)-dimensional spaces in this projective space contain a given t-dimensional space?
6. (solved by @nuuskur ) Let ##C## be a subspace of ##F_q^n##. We call ##C## cyclic if ##C## contains its right shifts, i.e. ##x = (c_1, \dots, c_n) \in C \implies \vec{x} = (c_n, c_1 \dots, c_{n-1}) \in C##. Show that there is a correspondence between the cyclic subspaces of ##F_q^n## and the ideals of the quotient ring ##F_q[X]/(X^n-1)##.
7. (solved by @nuuskur ) Let ##(W_t)_{t\geq 0}## be a Brownian motion on a suitable probability space. Put ##X:= \int_{0}^t W_s^2 ds##. Calculate ##E(X).## (changed, 7/5/19)
8. (solved by @nuuskur ) Calculate the Galois group of the splitting field of ##x^4 - 2x^2 -2## over ##\mathbb{Q}##. Determine the isomorph type of the Galois group.
9. Prove that every symmetric and positive definite matrix ##A\in \mathbb{M}(n,\mathbb{R})## can be uniquely written as ##A=L\cdot L^\tau##, where ##L## is a lower triangular matrix with positive diagonal elements.
Calculate ##L## for ##A=\begin{bmatrix}4 &2& 4& 4\\
2& 10& 17& 11\\
4& 17& 33& 29\\
4& 11& 29& 39\end{bmatrix}##.
10. (solved by @nuuskur ) Let ##L\subseteq H## be a nonempty, closed, and convex set in a Hilbert space. Prove that there is an element of minimal norm in ##L##.
11. (solved by @Physics lover ) Solve the following integral
$$I = \int_0^{\pi/2} \frac{\sin^{2019} x}{\cos^{2019} x + \sin^{2019} x}dx$$
12. (solved by @Pi-is-3 ) Is ##N:=21^{39}+39^{21}## divisible by ##45##? Why, why not?
13. (solved by @Pi-is-3 ) Let ##0<u,v,w<1##. Show that among the numbers ##u(1-v)\, , \,v(1-w)\, , \,w(1-u)## is at least one value not greater than ##\dfrac{1}{4}\,.##
14. (solved by @JosephFG ) What is the ratio between the red and the blue area where ##P## and ##Q## are one fifth away from the vertices?
15. (solved by @Pi-is-3 ) In what ratio does the circumference of the circle divide the left and right sides of the square?
Last edited: