Question Regarding Parallel Plate Capacitor Network

[jezza10181]

Homework Statement

Capacitor/Resistor network Question

Relevant Equations

Q = V * C

Hello,

I have a question regarding the capacitor/resistor network as shown.

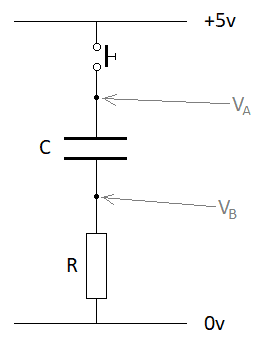
My question is simple. I realize that the instant the switch is closed, then the top plate of the capacitor must be at a potential (VA) of 5v.
However, I also realize that the instant the switch is closed, literally at time zero, then the capacitor must have zero charge on it. In that case, then the bottom plate must also be at a potential (VB) of 5v.

This also makes sense because for current to flow through the resistor, then there needs to be a potential difference across it. My question is this, how does the bottom plate of the capacitor acquire a potential of 5v? I don't understand how this happens on a 'microscopic' level. How does it happen?

Regards
Jeremy Watts

 

[BvU]

Hi,

There is one essential datum that is missing in your scenario: the charge on (or, if you want, the voltage over) the capacitor.

the capacitor must have zero charge on it

No. Not necessarily. The switch may have been closed before and re-opened after any posssible interval, leaving the capacitor at a voltage anywhere between 0 and 5 V. (bythe way, the symbol you use is for a button, never mind).

Or, in an extreme case, it may have been charged much higher than to +5V/C or lower than 0V/C.

If we restrict ourselves to the case you start with an uncharged capacitor -- which I gather you intend to -- the situation right after the circuit is closed is

Capacitor uncharged $\Rightarrow$ 0V over capacitor.
5V over capacitor + resistor $\Rightarrow$ 5V over resistor and a current 5V/R flows, which charges up the capacitor to the tune of 5V/R Coulombs per second.

But you know all that.

My question is this, how does the bottom plate of the capacitor acquire a potential of 5v?

Because the other plate of the uncharged capacitor is connected to + 5V is the straight answer.

Would you be less 'surprised' if the resistor would be absent from the circuit ? (i.e. the circuit open below the capacitor)

 

[jezza10181]

"If we restrict ourselves to the case you start with an uncharged capacitor -- which I gather you intend to -- the situation right after the circuit is closed is

Capacitor uncharged ⇒⇒ 0V over capacitor.
5V over capacitor + resistor ⇒⇒ 5V over resistor and a current 5V/R flows, which charges up the capacitor to the tune of 5V/R Coulombs per second.

But you know all that. " <<<< Then why say it?"Because the other plate of the uncharged capacitor is connected to + 5V is the straight answer. " <<< But why?

I can see that an E-field must be starting to grow within the capacitor once it starts charging up, but I cannot see how the lower plate acquires a potential of 5v, as it is not physically connected to the other plate, or the top rail.

 

[DaveE]

Electric current can flow across the open space between the capacitor plates. It's a bit counter-intuitive if you think of electricity as being like water flow or billiard balls. You are asking a very interesting and fundamental question, IMO.
What you can't do is instantly change the voltage across the capacitor, that would take an infinite amount of current. Your question isn't really any different than asking how does this capacitor increase it's voltage when it is charging from 2V to 2.1V after the switch has been closed for a while.
Your answer lies in learning about capacitors (and Electricity & Magnetism) from a physics book, web site, lecture, etc. At the advanced level, you could also learn about "Displacement Current", that's how the PhD physicists understand this.
At a simpler level, you can just believe that current can flow, but only according to the equations that govern how capacitors work: I = C⋅(dV/dt) ≈ C⋅(ΔV/Δt)

 

[jezza10181]

Thanks Dave, I did actually get halfway through a physics degree... many years ago now. I do also have an applied maths degree, so I am no stranger to calculus & differential equations.

Its simply that when I was in school I just learned the equations and how to apply them, and I never really got down to the nitty gritty of what was actually going on. But yes, I do remember the concept of 'displacement current', my memory of it is vague though. So you say this this to do with displacement current?

 

[lewando]

...but I cannot see how the lower plate acquires a potential of 5v, as it is not physically connected to the other plate, or the top rail.

While the lower plate is not connected to the upper plate (when the switch is open), the two plates are coupled by proximity and geometry. The degree of this coupling is the capacitance.

If you accept that you have a capacitor on your hands, then you probably accept that V = Q/C is a good governing equation. And so it follows that if Q = 0 (the assumed initial state in this case) then V, the voltage across the capacitor, will also be equal to 0.

The switch is then closed and the top plate is raised to at a potential of 5 V. At the very earliest moment, even before the first electron makes its transit around the circuit, the Q is unchanged (zero) and so the voltage across the capacitor is still zero. 5 V - 0 V = 5 V, like adding batteries. If the bottom plate had any other voltage at this instant it would be a result of additional Q materializing out of nowhere to change the voltage across the capacitor. This doesn't happen, of course.

Electric current can flow across the open space between the capacitor plates.

Not actual electrons. Unless the capacitor is being destructively overvoltaged.

 

[DaveE]

Not actual electrons. Unless the capacitor is being destructively overvoltaged.

OK, Hence my reference to Displacement current. Electric current doesn't have to be electrons. This is the magic of capacitors and James Clerk Maxwell. It's really an intriguing device which we often take for granted.
However, "current flow" is an an incredibly common and useful shorthand if you consider the "black box" view of the device. Electrons move into one plate and electrons leave the other in lock-step.
If you walk down the halls of the EE departments at Boeing, Intel, Volkswagon, etc. and say that current doesn't flow through a capacitor people will think you are a pedantic nerd. But in Physics Forums or an E&M lecture, your point is correct and appropriate.

 

[DaveE]

So you say this this to do with displacement current?

Yes

 

[lewando]

pedantic nerd

Who are you calling "pedantic"?



Had to look that one up just to be sure. Look, in this sub-forum, I assumed a B-level question/response. So I did not want to jump into any EM topics, off the bat. So my posts stand, look forward to any questions regarding them.

Best.

 

[DaveE]

Who are you calling "pedantic"?



Had to look that one up just to be sure. Look, in this sub-forum, I assumed a B-level question/response. So I did not want to jump into any EM topics, off the bat. So my posts stand, look forward to any questions regarding them.

Best.

Physics Forum - We're all pedantic nerds, that's kind of the point isn't it, LOL.

 

[jezza10181]

Yes

Just reminded myself about displacement current, and yes that makes total sense. Its a 'virtual current' that is associated with the magnetic field that is set up within the capacitor as the current starts to build. This displacement current to equal in fact to the current within the circuit, so this now makes sense.