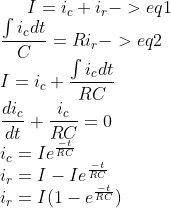SUMMARY
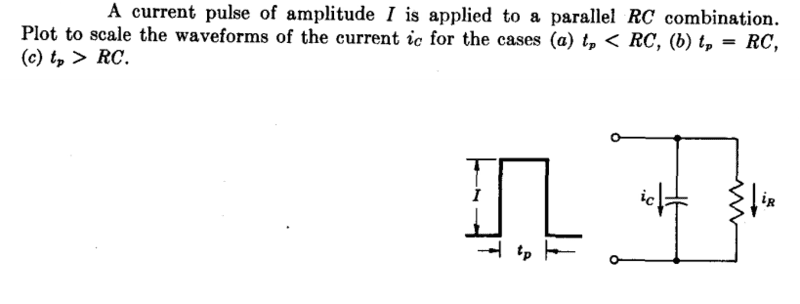
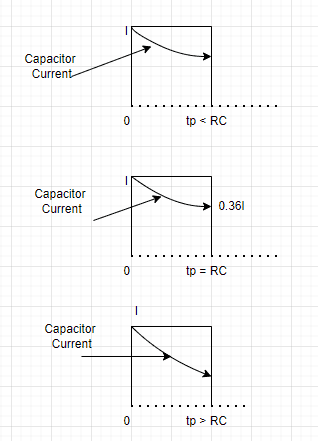
The discussion focuses on analyzing the behavior of a parallel RC circuit in response to a current pulse input. Key points include the impact of pulse duration (tp) relative to the time constant (RC) on current distribution between the resistor and capacitor. For very short pulses (tp << RC), most current flows through the capacitor; for very long pulses (tp >> RC), current predominantly flows through the resistor. Pulses around the time constant (tp ≈ RC) exhibit a mix of both behaviors, necessitating consideration of both components.
PREREQUISITES
- Understanding of RC circuit theory
- Familiarity with impedance concepts
- Knowledge of current pulse characteristics
- Basic grasp of exponential decay in electrical circuits
NEXT STEPS
- Study the effects of varying pulse widths on RC circuits
- Learn about the mathematical modeling of RC circuits using differential equations
- Explore practical applications of RC circuits in signal processing
- Investigate the role of frequency response in RC circuit behavior
USEFUL FOR
Electrical engineers, students studying circuit theory, and anyone interested in the dynamics of RC circuits in response to varying current inputs.