Relation between spin dephasing time T2* and spin relaxation time

[rafaelg7]

Homework Statement: spin dephasing time
Homework Equations: spin relaxation time

Hello, i have seen the next equation that relates the spin dephasing time of an ensemble of électrons T2* with the spin relaxation of a single electron T2, and I would like to know how it was deduced/proposed:

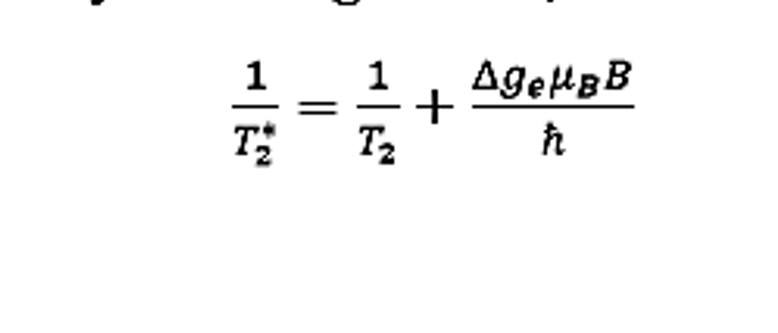
Thank you in advance

 

[marcusl]

It would be helpful if you included more information from your text, particularly what g_e is. I'm guessing that it's some type of coherence parameter. The "dephasing time" cannot be longer than the electron's relaxation time, and is shortened by decoherence of the ensemble. I imagine that g_e is related to the spatial field homogeneity.

 

[DrClaude]

It would be helpful if you included more information from your text, particularly what g_e is.

It is the electron spin g-factor.

@rafaelg7: The equation comes from the precession of an electron in a magnetic field. You will find a derivation in most QM textbooks (as often, I recommend Cohen-Tannoudji for this). You can also look up
https://en.wikipedia.org/wiki/Larmor_precession