Relative motion between cars with different types of movements

[Santilopez10]

Homework Statement

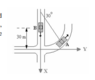
Car A drives a curve of radius 60m with a constant velocity of 48 km/h. When A is at the given position, car B is at 30m away from the intersection and accelerating at 1.2 m/s^2 to the south. Calculate the lenght and direction of the acceleration that car B would measure of car A from its perspective at that instant.

Relevant Equations

Kinematic equations in polar and cartesian coordinates

I think my approach is quite wrong, still I gave it a shot:
First I know that $v_A=13.3 m/s=r\omega=60\omega \rightarrow \omega=0.2 \frac{rad}{s}$
Then $$\vec a_A=-r\omega^2 e_r=-2.4 e_r$$
But $e_r=\cos{\theta}i+\sin{\theta}j$ and substituing the latter in the acceleration equation I have that $\vec a_A= -2i-1.2j$
At last: $$\vec a_{A/B}=\vec a_A - \vec a_B$$
and this is were I stopped, hope you can help me. Thanks!

 

[Emmo Amaranth]

Looks to me like you're on the right track. Someone else please correct me if I'm wrong, but this looks like a simple vector addition problem.

 

[Santilopez10]

Looks to me like you're on the right track. Someone else please correct me if I'm wrong, but this looks like a simple vector addition problem.

I believe it should be wrong because I am not even taking into account the y and x distance that are given to me as information, maybe I should add the relative angular speed of A from B, tbh I am not quite sure.

 

[Emmo Amaranth]

But should that matter? The question asks for instantaneous acceleration.

 

[Santilopez10]

not quite sure, that is why I am asking here.

 

[haruspex]

not quite sure, that is why I am asking here.

If car B were at a different point along the axis, none of the accelerations in the ground frame wouid change, so the relative acceleration cannot change.
But you should resist plugging in numbers straight away. Create variables to replace the given numbers and work symbolically, only plugging in numbers at the end. It has many advantages, one being precision. The answer you got is rather inaccurate.

 

[Santilopez10]

If car B were at a different point along the axis, none of the accelerations in the ground frame wouid change, so the relative acceleration cannot change.
But you should resist plugging in numbers straight away. Create variables to replace the given numbers and work symbolically, only plugging in numbers at the end. It has many advantages, one being precision. The answer you got is rather inaccurate.

Okay I ended with $$\vec{a_{A/B}}=(-\frac{v^2}{r}\cos{\theta}+1.2)i-\frac{v^2}{r}\sin{\theta} j$$
Plugging the values I get that $$\vec{a_{A/B}}=-1.36 i -1.5 j \rightarrow |\vec{a_{A/B}}|=2 \frac{m}{s^2} \rightarrow \vec{a_{A/B}}(\theta)=132º$$
Note I changed the axis so that Y points upwards and X points to the right if you were Car B.

 

[haruspex]

Okay I ended with $$\vec{a_{A/B}}=(-\frac{v^2}{r}\cos{\theta}+1.2)i-\frac{v^2}{r}\sin{\theta} j$$
Plugging the values I get that $$\vec{a_{A/B}}=-1.36 i -1.5 j \rightarrow |\vec{a_{A/B}}|=2 \frac{m}{s^2} \rightarrow \vec{a_{A/B}}(\theta)=132º$$
Note I changed the axis so that Y points upwards and X points to the right if you were Car B.

You have a sign error in the first equation above.

 

[Santilopez10]

You have a sign error in the first equation above.

Would you show me where? I am reading this at bed at the moment, it is 00:43 here . If I could afford making the noise to search for my stuff I would do it. (People sleeping here )

 

[haruspex]

Would you show me where? I am reading this at bed at the moment, it is 00:43 here . If I could afford making the noise to search for my stuff I would do it. (People sleeping here )

Are the two $\hat i$ accelerations in the same sense or opposite sense? Would you expect the relative acceleration to be more or less in magnitude then the max of the two?

 

[Santilopez10]

Are the two $\hat i$ accelerations in the same sense or opposite sense? Would you expect the relative acceleration to be more or less in magnitude then the max of the two?

You are right, it should be -1.2. Thanks a lot for the help!