Sarah0001
- 31
- 1
1.

E=mc^2
Relativistic mass equation given in the question
The first part of the question:
I understand 200 MeV is the energy lost as it initially moves with 200MeV however is brought to rest and thus this total kinetic energy must have been transferred from the 'two equal parts'
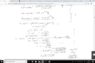
For the worked solution below,

Q : I am confused on how the total energy E=mc^2 = 200 MeV as implied in the work solution.
3. I thought
Ek = mc^2 - moc^2
does the worked solution instead mean that
delta theta = m - mo
and so delta theta = 200MeV/ c^2
The second Part of the question: What speed did the two masses have?

I see the worked solution rearranges the relativistic mass equation to make v the subject, it does this by using the approximation m = mo as delta m is so small
Q : however I am confused why they plug in 200*10^6 eV for delta m in the 2nd to last line of working shown.
Homework Equations
E=mc^2
Relativistic mass equation given in the question
The first part of the question:
I understand 200 MeV is the energy lost as it initially moves with 200MeV however is brought to rest and thus this total kinetic energy must have been transferred from the 'two equal parts'
For the worked solution below,
Q : I am confused on how the total energy E=mc^2 = 200 MeV as implied in the work solution.
3. I thought
Ek = mc^2 - moc^2
does the worked solution instead mean that
delta theta = m - mo
and so delta theta = 200MeV/ c^2
The second Part of the question: What speed did the two masses have?
I see the worked solution rearranges the relativistic mass equation to make v the subject, it does this by using the approximation m = mo as delta m is so small
Q : however I am confused why they plug in 200*10^6 eV for delta m in the 2nd to last line of working shown.
Attachments
Last edited by a moderator: