- #1
mainguy
- 15
- 0
Hi guys, thanks for helping with this! I'm a little stuck with this question about the derivation for relativistic mass.
1. Homework Statement
By considering the inelastic collision of two balls as perceived in different reference frames show that the relativistic mass is equal to the rest mass multiplied by the gamma factor (sqrt(1-u^2/c^2).
So I know the factor is 1/(1-u2/c2) but proving it is tough.
I've considered a reference frame moving at u in a direction perpendicular to the collision, so basically this:
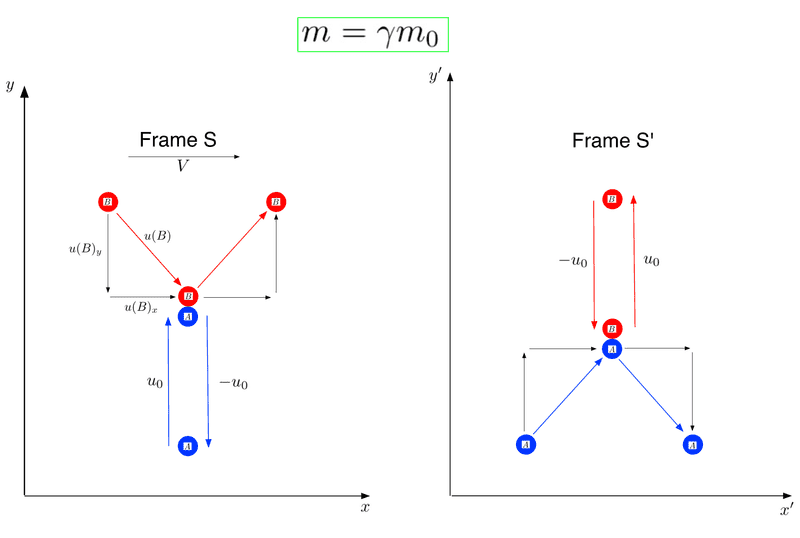
The vertical velocity u0 is transformed by a gamma factor, u = u'*gamma
So it slows down slightly as expected in the moving frame
It seems to me that the ball moving sidelong, say B in the first image, will have it's velocity altered in two parts. The vertical component will be multiplied by a gamma factor, and the horizontal component will transform as a lorentz:
u'= (u -v)/(1-uv/c2)
It seems clear to me that the vertical velocities of A and B are identical, and that they transform in an identical manner.
From class I know this isn't true, apparently they are identical velocities but they transform in a different manner. But I don't see how B could be transformed via the Lorentz formula if only a compnent of it's velocity is along the line parallel to the motion of the moving frame. Help would be much appreciated![/B]
1. Homework Statement
By considering the inelastic collision of two balls as perceived in different reference frames show that the relativistic mass is equal to the rest mass multiplied by the gamma factor (sqrt(1-u^2/c^2).
Homework Equations
So I know the factor is 1/(1-u2/c2) but proving it is tough.
I've considered a reference frame moving at u in a direction perpendicular to the collision, so basically this:
The Attempt at a Solution
The vertical velocity u0 is transformed by a gamma factor, u = u'*gamma
So it slows down slightly as expected in the moving frame
It seems to me that the ball moving sidelong, say B in the first image, will have it's velocity altered in two parts. The vertical component will be multiplied by a gamma factor, and the horizontal component will transform as a lorentz:
u'= (u -v)/(1-uv/c2)
It seems clear to me that the vertical velocities of A and B are identical, and that they transform in an identical manner.
From class I know this isn't true, apparently they are identical velocities but they transform in a different manner. But I don't see how B could be transformed via the Lorentz formula if only a compnent of it's velocity is along the line parallel to the motion of the moving frame. Help would be much appreciated![/B]
