SUMMARY
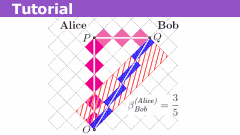
The discussion centers on the innovative use of rotated graph paper to teach relativity concepts, particularly in introductory classes. The method emphasizes constructing diagrams to enhance students' understanding of spacetime, moving away from traditional formula-heavy approaches like the Lorentz transformation. Participants noted that this visual method aids in grasping the operational interpretation of relativistic quantities, making it easier for students to draw and interpret spacetime diagrams. The conversation also highlights the challenges students face in diagramming and the potential benefits of using tools like GeoGebra for visualization.
PREREQUISITES
- Understanding of special relativity concepts such as spacetime diagrams and Lorentz transformations.
- Familiarity with Minkowski geometry and its differences from Euclidean geometry.
- Basic skills in using GeoGebra for creating visual representations of mathematical concepts.
- Experience with teaching methodologies in physics education.
NEXT STEPS
- Explore the use of GeoGebra for creating interactive spacetime diagrams.
- Research effective teaching strategies for introducing special relativity concepts in classrooms.
- Study the operational interpretation of relativistic quantities to enhance student comprehension.
- Review the article "Am. J. Phys. 84, 344-359 (2016)" for deeper insights into the discussed methods.
USEFUL FOR
Physics educators, curriculum developers, and anyone interested in innovative teaching methods for special relativity, particularly those looking to improve student engagement and understanding through visual tools.