Relativity Variables: Velocity, Doppler-Bondi k, and Rapidity - Comments

[robphy]

robphy submitted a new PF Insights post

Relativity Variables: Velocity, Doppler-Bondi k, and Rapidity

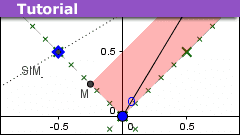
Continue reading the Original PF Insights Post.

 

[vanhees71]

In your story in the very beginning, your terminology is a bit unusual. The relative velocity of two particles is defined frame independently as the velocity of one particle in the rest frame of the other. What you where asking is the particles' velocity in the center-of-mass frame given $\beta_{\text{rel}}=0.5$!

 

[robphy]

Yes, I was probably a little sloppy.
I was thinking that one particle is at rest and the other moves with velocity 0.5c. What is the velocity of the center of momentum frame?

 

[pervect]

I believe that there is a typo in the insight, the proper expression for $\beta$ in terms of k is:

$$\beta = \frac{k^2-1}{k^2+1}$$

not

$$\beta = \sqrt{\frac{k^2-1}{k^2+1}}$$

I checked it a couple of different ways (including algebraic substitution). The second way involves tracing out light signals. If we imagine a signal emitted at t=1 , reflected off an observer moving at some velocity $\beta$, the signal comes back at time k^2. The distance at t=0- is 0. The radar results imply that the distance at time $(k^2+1)/2$ is equal to $(k^2-1)/2$, making the velocity the first expression without the square root.

 

[robphy]

@pervect , yes, that's a stray square root sign. Thanks.

 

[vanhees71]

Yes, I was probably a little sloppy.
I was thinking that one particle is at rest and the other moves with velocity 0.5c. What is the velocity of the center of momentum frame?

Yes, that's the right way to state it. It's important that relative velocity is a Lorentz-invariant quantity by defining it in a specific frame, i.e., the velocity of particle 1 in the rest frame of particle 2, and that's used in the definition of the cross-section formula, making the cross section an invariant quantity too.

Related are the somewhat confusing definitions of several invariant quantities like temperature and chemical potential in relativistic statistical/thermal physics or energy and momentum for non-closed systems, where the energy-momentum tensor is not conserved. The latter issue is carefully discussed in Jackson, Classical Electrodynamics.

 

[Greg Bernhardt]

Great job Rob!

 

[PeroK]

You can also do it using the energy momentum transformation. If particle 1 is at rest and particle 2 is moving at velocity $\beta$ (gamma factor $\gamma$) and the COM frame is moving at velocity $\alpha$ then:

$p'_1 = \gamma_{\alpha}m\alpha$

$p'_2 = \gamma_{\alpha}(\gamma m \beta - \gamma m \alpha)$

Equating the two momenta gives:

$\alpha = \frac{\gamma \beta}{1+\gamma} = \sqrt{\frac{\gamma -1}{\gamma +1}} = \frac{\beta}{1+\sqrt{1-\beta^2}}$

This method extends quite well for particles of different masses.

 

[PeroK]

...

$\alpha = \frac{\sqrt{\gamma^2-1}}{\gamma +\frac{m_1}{m_2}} = \frac{\beta}{\frac{m_1}{m_2}\sqrt{1-\beta^2}+1}$

 

[tom.capizzi]

I believe that there is a typo in the insight, the proper expression for $\beta$ in terms of k is:

$$\beta = \frac{k^2-1}{k^2+1}$$

not

$$\beta = \sqrt{\frac{k^2-1}{k^2+1}}$$

I checked it a couple of different ways (including algebraic substitution). The second way involves tracing out light signals. If we imagine a signal emitted at t=1 , reflected off an observer moving at some velocity $\beta$, the signal comes back at time k^2. The distance at t=0- is 0. The radar results imply that the distance at time $(k^2+1)/2$ is equal to $(k^2-1)/2$, making the velocity the first expression without the square root.

I believe that there is a typo in the insight, the proper expression for $\beta$ in terms of k is:

$$\beta = \frac{k^2-1}{k^2+1}$$

not

$$\beta = \sqrt{\frac{k^2-1}{k^2+1}}$$

I checked it a couple of different ways (including algebraic substitution). The second way involves tracing out light signals. If we imagine a signal emitted at t=1 , reflected off an observer moving at some velocity $\beta$, the signal comes back at time k^2. The distance at t=0- is 0. The radar results imply that the distance at time $(k^2+1)/2$ is equal to $(k^2-1)/2$, making the velocity the first expression without the square root.

The k-factor in Bondi's k-calculus is an eigenvalue of the Lorentz matrix which boosts relative velocity from rest to βc. Since k is never 0, we can divide both numerator and denominator by k, resulting in β = (k-1/k)/(k+1/k) = 2 sinh(w)/2 cosh(w) = tanh(w), because k = e^w. From common practice, β = sin(angle), implying that for all values of w, there exists a value of "angle" such that sin(angle) = tanh(w). This defines a relationship between circular rotation angles and hyperbolic rotation angles, a function known as the gudermannian. As a relationship between angles, it applies to all trig functions. Here's the list:
cosh(w) = sec(angle) = γ = 1/√(1-v²/c²) = c/√(c²-v²)
sinh(w) = tan(angle) = βγ = (v/c)/√(1-v²/c²) = v/√(c²-v²)
tanh(w) = sin(angle) = β = v/c
sech(w) = cos(angle) = 1/γ = √(1-v²/c²) = √(c²-v²)/c
csch(w) = cot(angle) = 1/(βγ) = √(1-v²/c²) / (v/c) = √(c²-v²)/v
coth(w) = csc(angle) = 1/β = c/v
For all pairs of angles where the circular angle is the gudermannian of the hyperbolic rotation angle, all 6 statements above are true. Verify for yourself by looking up trigonometric hexagon, or magic hexagon.

 

[robphy]

The k-factor in Bondi's k-calculus is an eigenvalue of the Lorentz matrix which boosts relative velocity from rest to βc. Since k is never 0, we can divide both numerator and denominator by k, resulting in β = (k-1/k)/(k+1/k) = 2 sinh(w)/2 cosh(w) = tanh(w), because k = e^w. From common practice, β = sin(angle), implying that for all values of w, there exists a value of "angle" such that sin(angle) = tanh(w). This defines a relationship between circular rotation angles and hyperbolic rotation angles, a function known as the gudermannian. As a relationship between angles, it applies to all trig functions. Here's the list:
cosh(w) = sec(angle) = γ = 1/√(1-v²/c²) = c/√(c²-v²)
sinh(w) = tan(angle) = βγ = (v/c)/√(1-v²/c²) = v/√(c²-v²)
tanh(w) = sin(angle) = β = v/c
sech(w) = cos(angle) = 1/γ = √(1-v²/c²) = √(c²-v²)/c
csch(w) = cot(angle) = 1/(βγ) = √(1-v²/c²) / (v/c) = √(c²-v²)/v
coth(w) = csc(angle) = 1/β = c/v
For all pairs of angles where the circular angle is the gudermannian of the hyperbolic rotation angle, all 6 statements above are true. Verify for yourself by looking up trigonometric hexagon, or magic hexagon.

Yes, this is true.
However, I prefer the hyperbolic functions because they are more natural for relativity
than these Euclidean functions (yes, related by the Gudermannian).

The end of my Insight
https://www.physicsforums.com/insights/relativity-variables-velocity-doppler-bondi-k-rapidity/
shows the connections between rapidity and the k-factor and the velocity-factor.
(I see now that this thread is a discussion of that Insight.)

 

[tom.capizzi]

I agree with your sentiments about hyperbolic functions. It appears to me that the universe prefers hyperbolic coordinates. The gudermannian function can be implemented with a classic Greek geometry ruler-and-compass construction. Through simple geometric operations, it is easy to demonstrate that the area on the graph which corresponds to rapidity is identical to the definite integral of 1/x, which is ln(x), if one limit is x=1. As a consequence of the rules of integration, rapidity composition is just linear addition, because of the property of the linear addition of the limits of definite integrals. Of all the variables that reference velocity, rapidity is the only one that combines linearly. Further analysis reveals that the non-linear velocity addition rule is merely a translation of the linear addition of rapidities from hyperbolic rotation angles to circular rotation angles and their trig functions. Similarly, the Lorentz Transform matrix itself is easily derived by applying the hyperbolic identities for the sum of two angles. It is for very good reasons that k-calculus is so appropriate for studying relativity. Among other reasons, it is based on the eigenvalues of the matrix. And no discussion of eigenvector decomposition would be complete without reference to the eigenvectors. But Bondi did not make the connection between his k-calculus and eigenvector decomposition. He did imitate it, however, with his radar measurements. After all, it isn't the radar that matters, per se. It is the fact that radar travels at the speed of light, which Einstein asserted was the same for all observers. The equations of the eigenvectors are ct+r=0 and ct-r=0, the world lines of photons. So, while Bondi used radar to make measurements, the coordinates in eigenvector space are determined by light rays, also traveling at the speed of light. If I explain what this means, PF moderation will call it "personal speculation", so I will merely call attention to the fact that the speed of light is invariant with respect to relative velocity of its source or the observer. Since position in eigenspace is measured by light rays, the measurements and the coordinates are also invariant. There is no trace of time dilation or length contraction in the rest frame of eigenspace. Others have mentioned the light rectangles of Mermin. He did not use eigenvector coordinates. As a result, his rectangles have areas that vary (predictably) with velocity. The coordinates in eigenspace are (ct+r,ct-r), and the area of the light rectangle becomes (ct+r)(ct-r) = c²t²-r² = s², the Einstein Interval, a known invariant. Everything about relativity is easier to grasp in eigenspace.

Earlier I remarked that the universe prefers hyperbolic coordinates. Hyperbolic magnitude is s, and hyperbolic rotation angle is rapidity, w. The hyperbolic magnitude is the Einstein interval in both Minkowski spacetime (where it is a vector) and eigenspace (where it is a bivector), while the hyperbolic rotation angle, rapidity, is the same in all three coordinate systems. The implications are an inconvenient truth to mainstream physics, and, apparently, PF moderators as well.

 

[robphy]

I agree with your sentiments about hyperbolic functions. It appears to me that the universe prefers hyperbolic coordinates. The gudermannian function can be implemented with a classic Greek geometry ruler-and-compass construction. Through simple geometric operations, it is easy to demonstrate that the area on the graph which corresponds to rapidity is identical to the definite integral of 1/x, which is ln(x), if one limit is x=1. As a consequence of the rules of integration, rapidity composition is just linear addition, because of the property of the linear addition of the limits of definite integrals. Of all the variables that reference velocity, rapidity is the only one that combines linearly. Further analysis reveals that the non-linear velocity addition rule is merely a translation of the linear addition of rapidities from hyperbolic rotation angles to circular rotation angles and their trig functions. Similarly, the Lorentz Transform matrix itself is easily derived by applying the hyperbolic identities for the sum of two angles. It is for very good reasons that k-calculus is so appropriate for studying relativity. Among other reasons, it is based on the eigenvalues of the matrix. And no discussion of eigenvector decomposition would be complete without reference to the eigenvectors. But Bondi did not make the connection between his k-calculus and eigenvector decomposition. He did imitate it, however, with his radar measurements. After all, it isn't the radar that matters, per se. It is the fact that radar travels at the speed of light, which Einstein asserted was the same for all observers. The equations of the eigenvectors are ct+r=0 and ct-r=0, the world lines of photons. So, while Bondi used radar to make measurements, the coordinates in eigenvector space are determined by light rays, also traveling at the speed of light. If I explain what this means, PF moderation will call it "personal speculation", so I will merely call attention to the fact that the speed of light is invariant with respect to relative velocity of its source or the observer. Since position in eigenspace is measured by light rays, the measurements and the coordinates are also invariant. There is no trace of time dilation or length contraction in the rest frame of eigenspace. Others have mentioned the light rectangles of Mermin. He did not use eigenvector coordinates. As a result, his rectangles have areas that vary (predictably) with velocity. The coordinates in eigenspace are (ct+r,ct-r), and the area of the light rectangle becomes (ct+r)(ct-r) = c²t²-r² = s², the Einstein Interval, a known invariant. Everything about relativity is easier to grasp in eigenspace.

Earlier I remarked that the universe prefers hyperbolic coordinates. Hyperbolic magnitude is s, and hyperbolic rotation angle is rapidity, w. The hyperbolic magnitude is the Einstein interval in both Minkowski spacetime (where it is a vector) and eigenspace (where it is a bivector), while the hyperbolic rotation angle, rapidity, is the same in all three coordinate systems. The implications are an inconvenient truth to mainstream physics, and, apparently, PF moderators as well.

I would say much of the mathematics you describe is correct and known, but maybe not well-known.
Of course, Bondi's primary audience, namely, the general public, would not appreciate talk of eigenspaces.

The problem you are running into is
this notion of the "rest frame of [the] eigenspace", suggestive of a rest frame for light.
I think such a notion has problems in terms of definition
so that one cannot assume that
"since massive-particles have rest frames
that massless-particles have rest frames."
https://www.physicsforums.com/threads/photons-perspective-of-time.107741/#post-899778

So, the math appears right... but it seems one has to draw the line... at the light-cone,
the boundary of the timelike 4-vectors...
unless one really pins down the definitions that would define a reference frame that I suggested in that old post.

 

[tom.capizzi]

I understand that there is no absolute rest frame. It is just awkward to talk about an eigenvector space which is at rest relative to whatever inertial frame was already chosen to be the reference frame. You know that you can't even talk about comparative measurements unless two inertial frames are synchronized. To do that, one frame must be defined to be the reference frame. Since inertial frames in general cannot be distinguished from an absolute rest frame (which is why we can't identify one), for all practical purposes, the reference frame becomes a de facto rest frame for all the other frames that are synchronized with it, as long as it remains inertial.