- #1
- 6,870
- 2,306
robphy submitted a new PF Insights post
Relativity using the Bondi k-Calculus
Continue reading the Original PF Insights Post.
Relativity using the Bondi k-Calculus
Continue reading the Original PF Insights Post.
About forty years before Einstein, Maxwell published equations describing electromagnetism. One solution to the equations was a wave, which turned out to have the properties of light. One weird thing was that the speed of the wave came out the same always. Naturally everyone assumed that the equations weren't quite right and the hunt was on to find the problem.skanskan said:Why does he assume the velocity of light is the same for all inertial observers?
bahamagreen said:To the degree that the diagram tends to suggest that movie duration is a proxy for time dilation... it looks like it only works with cases of increasing separation, not cases of approach. Students would notice this...
bahamagreen said:Alice's movie is seen by Bob to be in slow motion, and Bob's movie is seen by Alice to be in slow motion. That is similar to SR in which Alice's and Bob's clocks would measure to each other to run slow ... but all your diagrams are presenting the case of increasing separation of the inertial travelers.
To the degree that the diagram tends to suggest that movie duration is a proxy for time dilation... it looks like it only works with cases of increasing separation, not cases of approach. Students would notice this...
bahamagreen said:If these movies were youtube videos, there would be a time indicator rolling at the bottom of the screen, so for example, both Alice and Bob could see that Alice's movie indicates that it starts at 00:00:00 and increments to 00:60:00 at the end. Although Bob can't necessarily "view Alice's clock" , he can see by the video time index that in comparison to his own clock her video is running slow... suggesting that her time is slower relative to his (and likewise his to hers when he sends video to her).
When Alice and Bob approach each other, it looks like Bob is going to see Alice's movie running faster (shorter time), and Bob's movie will be seen by Alice to be running faster... so this is not similar to SR which would maintain that each measure each others clocks running slow.
Ibix said:About forty years before Einstein, Maxwell published equations describing electromagnetism. One solution to the equations was a wave, which turned out to have the properties of light. One weird thing was that the speed of the wave came out the same always. Naturally everyone assumed that the equations weren't quite right and the hunt was on to find the problem.
The next forty years were a bit confusing as no one could find anthing wrong. Experiments that were expected to help (e.g. Michelson and Morley) didn't work as predicted, but did provide some ad hoc patches. Einstein had the insight that if the (apparently daft) prediction that light always travels at the same speed for all inertial observers was correct then he could explain all of the confusion. So he made the assumption.
I'm not quite sure what you mean by this. In his 1905 paper Einstein calls the constancy of the speed of light a "principle", although it's more often referred to as a "postulate". Either way, it's something he assumed. It's the basis of his reasoning, yes, and it isn't necessary for light to travel at the invariant speed for there to be an invariant speed. But neither fact makes Einstein's postulates anything other than postulates.michall said:So he made the assumption
This puts it in the wrong light. Einstein was quite explicit: the constancy of the speed of light is not an assumption (an hypothesis or an empirical generalization). It is a bit of logic that has to do with the only possible way of synchronizing (distant) clocks and measuring time. It is a conceptual necessity, not a fact about the nature of light.
michall said:It is a bit of logic that has to do with the only possible way of synchronizing (distant) clocks and measuring time.
michall said:There is a circularity in the idea of measuring the speed of light: to measure the speed you need synchronized clocks; but you can't get distant clocks synchronized unless you know the speed of light. It's a logical circle.
The one-way speed of light, yes. That's why it's the two-way speed that is considered invariant. The one-way speed is conventionally assumed to be equal to the two-way speed, but there's no way to test this.michall said:There is a circularity in the idea of measuring the speed of light: to measure the speed you need synchronized clocks; but you can't get distant clocks synchronized unless you know the speed of light.
A way out of it. I derived some of the maths for inertial frames assuming otherwise here. It's not difficult, just ugly.michall said:The only way out of it, says Einstein, is to assume (stipulate) that the time it takes light to go from A to B = the time it takes to go from B to A.
Not quite; there are no empirically determinable values for the one way speed of light - that's why it's a convention. Choosing a value other than c is simply choosing a different (non-orthogonal) coordinate system in spacetime. Most people don't do it for inertial frames because it's ugly, unintuitive, makes the maths more complex, and adds nothing over the simple symmetric assumption - but there is nothing preventing it.michall said:Some scientists and philosophers take the "1/2" to be a variable, as if it were an arbitrary choice among a range of other possible values, making the definition into a convention. But there are no other possible, ie. empirically determinable, values,
Why do you think that this doesn't apply to one clock measurements of the round-trip speed of a ball? Or a sound wave? What's special about light that there is a "logical identity" with its behaviour but nothing else?michall said:and because it is a one clock measurement of a round-trip, the constancy of the speed of the sigal follows as a logical inference.
Are you aware that the Bondi approach is a half-hearted attempt at eigenvector decomposition? The k-factor in Bondi k-calculus is, in fact, an eigenvalue of the Lorentz matrix. The radar measurements are another feature of eigenvector analysis, because the eigenvectors of the 2x2 Lorentz matrix are ct+r=0 and ct-r = 0. Note to PF moderators. That is not my opinion, that's a fact. Look it up. Other than those lines are identical to the worldlines of photons, and are built-in radar (or lidar) measurements, I can't say more. PF moderators think that mathematical analysis is my "personal opinion", and gave me non-expiring demerits for posting math. I would close my account, but their privacy policy won't let me. So I will continue to post inconvenient mathematical truth until they ban me for life, which I will accept as a badge of honor. This site is too conservative.robphy said:Any approach I use must use the spacetime diagram
because I think it is difficult to represent the relativity-of-simultaneity using boxcars as "moving frames of reference".
Any approach I use must use radar methods
to motivate measurements and the assignment of coordinates.
I think radar methods are more straightforward than lattices of "clocks" and "rods".
(For inertial motions in special relativity, they are equivalent.
However, for more general motions in special and general relativity, they may differ...
and would require more advanced discussion to address.)
In my opinion, the Bondi k-calculus method (with its emphasis on radar measurements) is the best starting point, especially for algebra-based physics. With the k-calculus methods, the standard textbook formulas are straightforward to derive and fall out naturally.
A related but even less well known approach by Geroch (in his General Relativity from A to B) is also a good starting point. Geroch uses radar methods to emphasize the square-interval and give operational interpretations of the geometry of spacetime (e.g., what simultaneity means to an observer) in both Special Relativity and Galilean Relativity. My AJP article (which inspired the Insight https://www.physicsforums.com/insights/relativity-rotated-graph-paper/ ) was my attempt to combine Bondi's and Geroch's approaches.
From here, I would go on to develop the geometry of Minkowski spacetime, while comparing and contrasting with Euclidean geometry, using the [unappreciated] geometry of Galilean spacetime (e.g., https://www.desmos.com/calculator/ti58l2sair ... play with the E-slider) ...something I call "Spacetime Trigonometry", a large ongoing project with many aspects which generates lots of posters for me at AAPT meetings. (I should really write this up soon... but it would have to be broken into a series of AJP articles.) These are examples of Cayley-Klein geometries, which includes the deSitter spacetimes.. This "unification" can help formalize the numerous analogies mentioned in the literature. In addition, I can develop vector and tensorial methods (algebraically, graphically, and geometrically) in order to make contact with traditional intermediate and advanced presentations of relativity.
I'm not sure what you mean by half-hearted...tom.capizzi said:Are you aware that the Bondi approach is a half-hearted attempt at eigenvector decomposition? The k-factor in Bondi k-calculus is, in fact, an eigenvalue of the Lorentz matrix. The radar measurements are another feature of eigenvector analysis, because the eigenvectors of the 2x2 Lorentz matrix are ct+r=0 and ct-r = 0. Note to PF moderators. That is not my opinion, that's a fact. Look it up. Other than those lines are identical to the worldlines of photons, and are built-in radar (or lidar) measurements, I can't say more. PF moderators think that mathematical analysis is my "personal opinion", and gave me non-expiring demerits for posting math. I would close my account, but their privacy policy won't let me. So I will continue to post inconvenient mathematical truth until they ban me for life, which I will accept as a badge of honor. This site is too conservative.
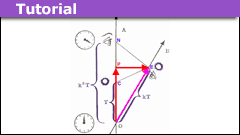
robphy said:These are related to “light-cone coordinates“, the coordinates in the eigenbasis of the Lorentz Transformation. In my convention, Δu=Δt+Δxc and Δv=Δt−Δxc. So, these equations can be rewritten as Δu=k^2T and Δv=T, The k-factor is an eigenvalue of the Lorentz Transformation
https://www.physicsforums.com/insights/relativity-using-bondi-k-calculus/
robphy said:The Doppler-Bondi k-factor is the eigenvalue along the future-forward direction, which stretches the light-clock diamond in that direction by a factor k. The reciprocal [itex] k^{−1} [/itex] is the eigenvalue along the future-backward direction, which shrinks the light-clock diamond by a factor of k. Note the light-clock diamond area is preserved. This is the basis of my “Relativity on Rotated Graph Paper” Insight.
Source https://www.physicsforums.com/insights/relativity-variables-velocity-doppler-bondi-k-rapidity/
The Bondi k-Calculus is a mathematical framework used to study the theory of relativity, specifically for gravitational waves in the context of general relativity. It was developed by Hermann Bondi in the 1960s and is based on the concept of null hypersurfaces.
The Bondi k-Calculus differs from other approaches, such as the traditional tensor calculus, by using null coordinates and null hypersurfaces instead of spacetime coordinates. This allows for a more elegant and efficient way to describe and analyze gravitational waves.
The Bondi k-Calculus offers several advantages, including simplifying the calculations involved in studying gravitational waves, providing a more intuitive understanding of the physical processes involved, and allowing for a more direct comparison with observations.
While the Bondi k-Calculus was originally developed for the study of gravitational waves, it has also been used in other areas of physics, such as cosmology and astrophysics. It offers a powerful mathematical tool for understanding and analyzing various phenomena in the universe.
One limitation of the Bondi k-Calculus is that it is primarily applicable to vacuum spacetimes, meaning those without matter or radiation. It also requires a high level of mathematical understanding and expertise to apply effectively.