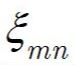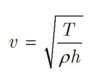Resonant frequencies of a membrane, dependance on Young's modulus?

[kravky]

Hello,

natural frequencies of (circular) membrane are expressed in every textbook as:

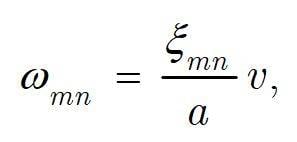
where

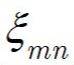is the m-th positive root of the Bessel Function of the first kind of order n. For m=1, n=0: ξ_mn = 2,405.

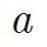represents the radius of membrane, and

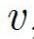is the velocity of wave propagation (transverse).

in every book there is an equation for velocity as follows:

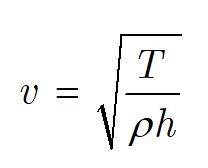where

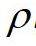is the density of membrane,

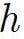represents the thickness of the membrane and

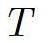is tension: force per unit length - dimension is therefore Newtons per meter.

I want to focus on the Tension. From the equations we can see, that the natural freq. depends on tension which makes sense. However how can i know the tension of the membrane? e.g tension of the ear drum, or tension of the membrane in microphone..

When we run FEM modal analysis in some program, we need only specify the geometry (radius) and material properties, such as Youngs modulus E, poissonous ratio and the density, and the program succesfully finds the natural modes of a membrane (e.g. clamped membrane). So my question is: How the program knows the tension? How can the software calculate the frequencies and mode shapes?

Is there a possibility to express natural freq. of membrane in terms of Youngs modulus, poissonous ratio, density, thickness, radius INDEPENDENTLY ON THE PRESTRESS (PRETENSION) ?

How Youngs modulus depends on the pretension? is there any relationship behind it?

Because in FEM we can see clear eveidence, that natural freq. does depend on the Youngs modulus E. However the equation in books does not contain Youngs modulus. It means that something is worng ?
Imagine we set in FEM simulation some pretension and we choose a value for Youngs modolus and so on... If we change the Youngs modulus the natural freq. will change however the equation says it will not change :-D

I don't understand physics behind this finding of natural freq. Maybe i don't understand what this tension means.

If You could help me, i would appreciate it greatly.

 

[Chestermiller]

From your equation, what are the units of T?

 

[kravky]

The units of T are [N/m]. It means it is a force per unit length (Newtons/metres). unit of h is meter [m] and the units of rho are [kg/m^3].

 

[Chestermiller]

The units of T are [N/m]. It means it is a force per unit length (Newtons/metres). unit of h is meter [m] and the units of rho are [kg/m^3].

This is correct. So the physical interpretation of T is tensile stress times thickness, or force per unit length along any segment of cut within the plane of the membrane. Along the rim of the membrane, T is the tensile force per unit length around the circumference.