Resultant Force and its Components

[Auburn2017]

Homework Statement

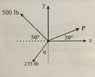
The Resultant of the system of forces shown is R = 425 j lbs. Determine the possible values of P and Θ.

Homework Equations

R = F1 +F2+P

The Attempt at a Solution

I ended up with two equations, one in the "i" direction and one in the "j" direction. I think you have to use the quadratic formula because I know that you will get two values for P and two values for Θ. Thanks!

 

[BiGyElLoWhAt]

So what's the problem? What specifically?

 

[Auburn2017]

So what's the problem? What specifically?

The Problem is to find P and Θ. You will need to refer to the figure I attached on the original post. I get two equation but then I can't get past that point.

 

[BiGyElLoWhAt]

2 equations, 2 unknowns? Solve for one of the variables and use substitution.

 

[BiGyElLoWhAt]

Example:
$a = x + y$
$b = 2x - 3y$
Solve for x in the first equation:
$x= a- y$
Sub it into the second equation for x
$b = 2(a-y) - 3y$
Then solve for y.
Once you have found y, plug it into one of the equations and solve for x.

 

[SteamKing]

2 equations, 2 unknowns? Solve for one of the variables and use substation.

Or substitution.

 

[BiGyElLoWhAt]

... fixed

 

[Auburn2017]

2 Equation and 2 unknowns should result in an answer for P and an answer for Θ. The solution has two answers for P and two answers for Θ.

 

[Auburn2017]

Can someone please just solve this problem?

 

[BiGyElLoWhAt]

That's against policy, sorry. I'm not seeing multiple solutions. It's kind of a mess, but I only see one solution for theta. Use the trig identity sin(theta) = cos(theta +90) or vice versa cos(theta) = sin(theta - 90), then factor, and solve.

 

[Auburn2017]

That's against policy, sorry. I'm not seeing multiple solutions. It's kind of a mess, but I only see one solution for theta. Use the trig identity sin(theta) = cos(theta +90) or vice versa cos(theta) = sin(theta - 90), then factor, and solve.

Yeah that's what I have done and only got one solution. Unfortunately the solution manual says that P=545.46 and 53.89, Θ=33.30° and -87.44°

 

[SteamKing]

Yeah that's what I have done and only got one solution. Unfortunately the solution manual says that P=545.46 and 53.89, Θ=33.30° and -87.44°

If you take the original force diagram and decompose the vectors shown into components, you should obtain two equations in P and θ. You know the x-component of the resultant is equal to 0, while the y-component must equal 425 lbs. Further algebraic manipulation yields and equation in sin θ and another in cos θ. By squaring and adding these two equations together, one can use the Pythagorean relation to eliminate θ, leaving a quadratic in P, which of course gives two values as solutions.

By substituting these values of P back into one of the earlier equations involving θ, you can obtain a pair of angles which are also solutions, but only one angle will work with a given solution to P, while the other angle works with the other solution to P. This is why there are four answers given.

Now, instead of dancing around this problem, if you would like to share your work towards solution, we may be able to see where you went wrong in your original attempt.

 

[Auburn2017]

If you take the original force diagram and decompose the vectors shown into components, you should obtain two equations in P and θ. You know the x-component of the resultant is equal to 0, while the y-component must equal 425 lbs. Further algebraic manipulation yields and equation in sin θ and another in cos θ. By squaring and adding these two equations together, one can use the Pythagorean relation to eliminate θ, leaving a quadratic in P, which of course gives two values as solutions.

By substituting these values of P back into one of the earlier equations involving θ, you can obtain a pair of angles which are also solutions, but only one angle will work with a given solution to P, while the other angle works with the other solution to P. This is why there are four answers given.

Now, instead of dancing around this problem, if you would like to share your work towards solution, we may be able to see where you went wrong in your original attempt.

This is what I have gotten so far.

 

[SteamKing]

This is what I have gotten so far.

This looks good.

Re-write the two final equations so that sin θ and cos θ are on one side with P and the rest on the other side of the equals.

Square the LHSides and eliminate θ using the Pythagorean relation, sin² θ + cos² θ = 1.

After that, it becomes a matter of collecting the remaining terms and writing a quadratic equation in P.

 

[Auburn2017]

This looks good.

Re-write the two final equations so that sin θ and cos θ are on one side with P and the rest on the other side of the equals.

Square the LHSides and eliminate θ using the Pythagorean relation, sin² θ + cos² θ = 1.

After that, it becomes a matter of collecting the remaining terms and writing a quadratic equation in P.

So you are saying I can square both sides and then set the RHSides equal to one? and then solve for P using quadratic equation?

 

[Auburn2017]

This looks good.

Re-write the two final equations so that sin θ and cos θ are on one side with P and the rest on the other side of the equals.

Square the LHSides and eliminate θ using the Pythagorean relation, sin² θ + cos² θ = 1.

After that, it becomes a matter of collecting the remaining terms and writing a quadratic equation in P.

I did that and got some extremely small numbers for P

 

[SteamKing]

I did that and got some extremely small numbers for P

Then you made some mistakes somewhere in you calculations.

So you are saying I can square both sides and then set the RHSides equal to one? and then solve for P using quadratic equation?

Not necessarily. You have one equation in sin θ and another equation in cos θ. By squaring these two equations and adding them together, you wind up with a third equation where you have something like A (sin² θ + cos² θ) = RHS with P terms. sin² θ + cos² θ = 1 by the Pythagorean relation, and the terms involving θ drop out.

 

[SammyS]

So you are saying I can square both sides and then set the RHSides equal to one? and then solve for P using quadratic equation?

From your work:

Isolate the terms with sin(θ) and cos(θ) on one side of each equation. You can leave each with a coefficient of 275 .

You may want leave .866 as $\displaystyle\ \frac{\sqrt3} {2}\ .$

Be careful in squaring the other side. It will have two terms. Remember: $\ (a-b)^2=a^2-2ab+b^2\ .$

 

[SammyS]

Another method of solution you may want to consider can be done using a graphing calculator, such as a TI-83 or TI-84 .

Solve each equation for P.
The first equation gives P as some function of θ, the other equation gives P as some other function of θ.

With the TI calculators, P of the first equation will be treated as Y₁ , and P of the second equation will be treated as Y₂. In both cases use X in place of θ .

I suppose you should leave the calculator in DEGREE mode.
Use the trig ZOOM to set the X scale. You may need to fiddle with the Y scale. It looks like the Y range should be about ±750 .

Once the graphs look good, use the intersect feature of the calculator.

 

[Auburn2017]

Then you made some mistakes somewhere in you calculations.

Not necessarily. You have one equation in sin θ and another equation in cos θ. By squaring these two equations and adding them together, you wind up with a third equation where you have something like A (sin² θ + cos² θ) = RHS with P terms. sin² θ + cos² θ = 1 by the Pythagorean relation, and the terms involving θ drop out.

I got here and then I add the RHSide together correct? and set that equal to 1? Because when I do that you start getting extremely small numbers...

 

[Chestermiller]

Another way to solve this is to solve for P in the j equation, and substitute the result into the i equation. You then have an equation involving the sum of terms involving cosine and sine. These can be combined into a single term by using the sine of the sum of two angles trig formula.

Chet

 

[SammyS]

I got here and then I add the RHSide together correct? and set that equal to 1? Because when I do that you start getting extremely small numbers...

What did you do with these in order to get your very small numbers?

 

[Auburn2017]

What did you do with these in order to get your very small numbers?

I carried out the squared operation on the RHS for both equations. Then I added them together and set it equal to one since sin²Θ + cos²Θ=1. Then I solved for P

 

[SammyS]

I carried out the squared operation on the RHS for both equations. Then I added them together and set it equal to one since sin²Θ + cos²Θ=1. Then I solved for P

It may have been easier to leave the 275 as coefficient of cos(θ) and sin(θ) .

At any rate, can you show what you get by squaring the right hand sides before you add them?

 

[Auburn2017]

It may have been easier to leave the 275 as coefficient of cos(θ) and sin(θ) .

At any rate, can you show what you get by squaring the right hand sides before you add them?

Yes I can. How does leaving the 275 as a coefficient change the procedure?

 

[SammyS]

Yes I can. How does leaving the 275 as a coefficient change the procedure?

Adding those should give something like:

$\displaystyle 1=( 321.39^2+ 41.98^2-2((321.39)(.866)+(41.98)(0.5))P+P^2)/275^2$​

or its equivalent..

 

[Auburn2017]

View attachment 102608

Adding those should give something like:

$\displaystyle 1=( 321.39^2+ 41.98^2-2((321.39)(.866)+(41.98)(0.5))P+P^2)/275^2$​

or its equivalent..

I do not see how your last term there would just be P²?

View attachment 102608

Adding those should give something like:

$\displaystyle 1=( 321.39^2+ 41.98^2-2((321.39)(.866)+(41.98)(0.5))P+P^2)/275^2$​

or its equivalent..

Thank You! Can I not just multiple both sides by 275^2 and then subtract that number from the left side so then I will have 3 terms added equal to zero?

 

[Auburn2017]

I do not see how your last term there would just be P²?

Thank You! Can I not just multiple both sides by 275^2 and then subtract that number from the left side so then I will have 3 terms added equal to zero?

I FINALLY GOT THE ANSWER! THANK YOU SO SO MUCH!

 

[SammyS]

I do not see how your last term there would just be P²?

Thank You! Can I not just multiple both sides by 275^2 and then subtract that number from the left side so then I will have 3 terms added equal to zero?

$\displaystyle \left(\frac12 \right)^2+ \left( \frac{\sqrt{3}}{2} \right)^2=1$

 

[Chestermiller]

Here's the alternate method I alluded to in post #21:

$$-321.39-275\sin \theta+\frac{\sqrt{3}}{2}P=0\tag{1}$$
$$383.02-275\cos \theta + \frac{1}{2}P=425\tag{2}$$
Multiplying Eqn. 2 by $\sqrt{3}$ and subtracting yields:
$$383.02\sqrt{3}+321.39+550\left[\frac{1}{2}\sin \theta-\frac{\sqrt{3}}{2}\cos \theta\right]=425\sqrt{3}\tag{3}$$
Rearranging yields:
$$383.02\sqrt{3}+321.39-425\sqrt{3}=248.68=550(\cos \theta \cos 30-\sin\theta \sin 30)=550 \cos(\theta + 30)$$
Therefore, $$\cos(\theta + 30)=\frac{248.68}{550}=0.452$$