Mentz114
- 5,429
- 292
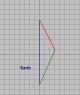
Each worldline taken between two events, has a unique proper time associated with it.Austin0 said:OK How do you distinguish between two inertial frames where the worldlines are totally reciprocal mirror images of each other?
I don't follow you. Any segment of any worldline has a proper time.WHere the passage of proper time is equivalent in each diagram as depicted by the length of the worldline how do you decide which one is accurate?
How do you explain the length of a piece of string ?Given kev's three inertial frames; if in fact you derive a difference in elapsed time between frames how do you explain this without an implication of actual motion on the part of some frame??
You're making a puzzle where there isn't one. Observing a moving clock may give you the impression that it is running slower than yours, but that's an instantaneous velocity dependent measurement. To get the proper time you have to integrate ( sum the infinitesimals) of this factor over the whole journey. It's a postulate of SR that this gives the correct elapsed time on the local clock.Out of curiosity what are you talking about " my persisting in ignoring proper time"
ANd what do you mean time dilation has nothing to do with elapsed time on clocks??
Do you think time dilation has nothing to do with the slope of worldlines and vice versa?
The Wiki page is not bad, I recommend a quick look.
http://en.wikipedia.org/wiki/Proper_time
Last edited: