How to measure time in reference frame with clock?

[Mike_bb]

TL;DR Summary

Time in reference frame with clock

I considered example of time dilation with light clock. I have a question about measuring time in reference frame with clock.

If we know that clock move from A to B in the reference frame with clock then what time of motion is measured in this reference frame? (In non-moving reference frame time is Δt)

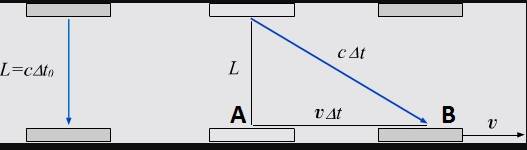
I supposed that time is Δt0 because light reach at end point at this time. But I think it's wrong. I have no more guess.

Thanks.

 

[PeterDonis]

I supposed that time is Δt0 because light reach at end point at this time. But I think it's wrong.

It's obviously wrong from your diagram, because the distance covered by the light beam in the moving light clock is not $c \Delta t_0$, it's $c \Delta t$. Which should make the time it takes in the given frame for the light beam to cover that distance obvious.

 

[Ibix]

Don't guess, compute!

Where is the light pulse when the clock is at A? Where is the light pulse when the clock is at B? How far has the light travelled, therefore? Hence, how long has it taken?

 

[Mike_bb]

Sorry. Picture in the first message is wrong.

 

[PeterDonis]

Picture in the first message is wrong.

What has changed? The picture you just posted looks the same as the one in the OP.

 

[Mike_bb]

What has changed? The picture you just posted looks the same as the one in the OP.

I mean that vΔt is length of path in non-moving reference frame (time in this frame is Δt). And what is time in reference frame with clock?

 

[PeterDonis]

I mean that vΔt is length of path in non-moving reference frame (time in this frame is Δt).

Yes. So that's the time the light takes to travel from A to B in the non-moving frame, if the clock is moving in that frame.

And what is time in reference frame with clock?

Do you mean the frame in which the clock is at rest? Isn't that what you've drawn in the left part of your diagram?

 

[Mike_bb]

Do you mean the frame in which the clock is at rest? Isn't that what you've drawn in the left part of your diagram?

No. I mean moving frame with velocity v and with moving clock.

 

[PeterDonis]

No. I mean moving frame with velocity v and with moving clock.

Then what does the left part of your diagram represent?

 

[Mike_bb]

Then what does the left part of your diagram represent?

It represent rest frame with zero velocity with rest clock. But I mean right diagram when I say about moving frame.

 

[PeterDonis]

It represent rest frame with zero velocity with rest clock.

And that means it represents any light clock with the same parameters (i.e., the same $L$ between its mirrors) in the frame in which it is at rest.

I mean right diagram when I say about moving frame.

Yes, a frame in which the clock is moving. But now you are asking about a frame in which the clock is at rest. Which is exactly what the left diagram shows. See above.

 

[Mike_bb]

But now you are asking about a frame in which the clock is at rest.

Ok. I ask about time in moving frame. I want to know time of motion from A to B in moving reference frame. In the rest frame time is Δt.

 

[PeterDonis]

I want to know time of motion from A to B in moving reference frame.

What do you mean by "moving reference frame"? You appear to mean a frame that is moving at the same $v$ as the clock. That means the clock is at rest in that frame.

 

[Mike_bb]

That means the clock is at rest in that frame.

Sorry, it's my error. Yes. Clock in moving frame is at rest. And I want to know what time is measured by clock in this moving frame.

 

[PeterDonis]

Clock in moving frame is at rest. And I want to know what time is measured by clock in this moving frame.

Since the clock is at rest in the frame, the left side of your diagram represents what happens. That is the point I have been trying to get across to you. So you can just look at the left side of your diagram to get the answer to your question.

 

[Mike_bb]

Since the clock is at rest in the frame, the left side of your diagram represents what happens. That is the point I have been trying to get across to you. So you can just look at the left side of your diagram to get the answer to your question.

I wrote that time is Δt0, is it true? But I'm confused because if we're moving from A to B then our distance is vΔt for our reference frame. And if time is Δt0 then distance is vΔt0. It's wrong result.

 

[PeterDonis]

I wrote that time is Δt0, is it true?

For the case where the clock is at rest, that is what the left part of your diagram says, yes.

I'm confused because if we're moving from A to B then our distance is vΔt for our reference frame. And if time is Δt0 then distance is vΔt0. It's wrong result.

No, it isn't, you're confusing two different things: the time taken in a frame in which the clock is moving, and the time taken in a frame in which the clock is at rest. Your use of the term "moving frame" to denote a frame in which the clock on the right of your diagram is at rest is probably contributing to your confusion.

Perhaps it will help you to think of two separate clocks. In the diagram you have drawn, the clock on the left is at rest and the clock on the right is moving. So in that frame, the time it takes the light beam in the left clock is $t_0$, and the time it takes the light beam in the right clock is $t$.

But you could also draw another diagram, in the frame in which the right clock is at rest. In this diagram, on the right there would be a clock at rest (the one that's on the right and moving in your original diagram), and on the left there would be a clock moving to the left with speed $v$ (the one that's on the left in your original diagram). And in that diagram, drawn in a different frame, the time it takes the light beam in the right clock would be $t_0$, and the time it takes the light beam in the left clock would be $t$.

 

[Mike_bb]

the time taken in a frame in which the clock is moving, and the time taken in a frame in which the clock is at rest.

Why do you say about light beam? I mean another case. Say what time do you measure in moving frame when you travel from A to B?

 

[PeterDonis]

Why do you say about light beam?

Um, because your diagram is a diagram of a light clock?

I mean another case. Say what time do you measure in moving frame when you travel from A to B?

The light clock is a clock; it measures time--the time it takes the light beam to go back and forth between its mirrors. That time is the time you have been asking about.

 

[Ibix]

This conversation seems enormously confusing.

The diagram in #1 has two clocks, the one on the left which is stationary in the frame in which the diagram is drawn, and the one on the right which is moving to the right with velocity $v$. In this frame, the period of the left clock is $\Delta t_0$ (well, twice that actually because the light pulse needs to travel down and up, but it doesn't matter here). The period of the clock on the right is $\Delta t$, which turns out to be $\left(1-v^2/c^2\right)^{-1/2}\Delta t_0$.

As far as I can work out, OP is asking what are the periods of the two clocks in a frame where the right clock is stationary and the left clock is moving to the left with speed $v$ (i.e. velocity $-v$). If that is correct, then the answer is simply that the periods swap: now the right clock has period $\Delta t_0$ and the left clock has period $\Delta t$.

Does that answer the question?

 

[Mike_bb]

Ok. I'll try to rephrase.

Let's write equation for non-moving reference frame:

$(cΔt)^2 = (cΔt0)^2 + (vΔt)^2$

How to write equation for moving reference frame?

 

[Ibix]

How to write equation for moving reference frame?

Do you mean the frame where the right hand clock is at rest? And how are you arriving at that equation? Are you just applying Pythagoras' Theorem to the triangle I've marked in red below?

 

[Mike_bb]

Thanks to all! My mistake was that I tried to find time of motion in moving frame but distance in this frame is 0 because clock in moving frame is at rest.