Rigid Objects Homework: Minimum Tipping Force & Friction Coefficient Calculation

  • Thread starter Thread starter iamhoms
  • Start date Start date
Click For Summary
SUMMARY

The discussion centers on calculating the minimum tipping force and the coefficient of static friction for a cabinet weighing 430 N with a width of 54.0 cm and a height of 100.0 cm. The first part requires determining the minimum force needed to initiate tipping, while the second part focuses on finding the static friction coefficient necessary to prevent sliding under this force. The third part involves calculating the minimum force required to tip the cabinet from any point of application. Key concepts include torque and static friction.

PREREQUISITES
  • Understanding of torque and its calculation
  • Knowledge of static friction and its coefficient
  • Familiarity with the concepts of force and weight
  • Basic principles of equilibrium in rigid body mechanics
NEXT STEPS
  • Study the calculation of torque in rigid body systems
  • Learn about static friction and its role in preventing motion
  • Explore the concept of moment of inertia in relation to tipping forces
  • Review examples of equilibrium problems involving tipping and sliding
USEFUL FOR

Students in physics, particularly those studying mechanics, engineers involved in structural design, and anyone interested in understanding the dynamics of rigid bodies under force.

iamhoms
Messages
2
Reaction score
0

Homework Statement


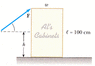
The cabinet in the figure below weighs 430 N and has width w = 54.0 cm. A force F is applied horizontally at the upper edge.
The height l = 100.0 cm.

(a) What is the minimum force that must be applied for the cabinet to start tipping?

(b) What is the minimum coefficient of static friction required to prevent the cabinet from sliding with the application of a force of this magnitude?

(c) Find the magnitude and direction of the minimum force required to tip the cabinet if the point of application can be chosen anywhere on it.


Homework Equations



The Attempt at a Solution


I do not have any idea on how to do this. I'm assuming it involves friction, torque, and possibly moment of inertia, but regardless I do not know where to start. Any help would be appreciated.
-James
 
Physics news on Phys.org
Include the figure please.
 
Cilabitaon said:
Include the figure please.

Do you mean a picture of the problem?
It is a rectangular cabinet. I'll attach a picture.
 

Attachments

  • p12-53alt.gif
    p12-53alt.gif
    13 KB · Views: 319

Similar threads

Calculating force to tip over a cabinet (static equilibrium)
  • · Replies 11 ·
Replies
11
Views
5K
Push/Pull Force of wheeled cart on an incline
  • · Replies 7 ·
Replies
7
Views
5K
Friction - problem with one of the equilibrium equations
  • · Replies 13 ·
Replies
13
Views
2K
Acceleration of object with friction: Homework help
  • · Replies 1 ·
Replies
1
Views
2K
How is the minimum work needed to push a car up an inclined plane calculated?
  • · Replies 4 ·
Replies
4
Views
3K
Rotational Torque, Forces, Tipping
  • · Replies 1 ·
Replies
1
Views
3K
Finding Minimum Force Needed to Hold Object In Place
  • · Replies 5 ·
Replies
5
Views
10K
Question Concerning The Coefficient of Friction: Block on a Rough Inclined Plane
  • · Replies 5 ·
Replies
5
Views
2K
Minimum force to make box slide down slope
  • · Replies 2 ·
Replies
2
Views
2K
How to find the coefficient of kinetic friction
  • · Replies 4 ·
Replies
4
Views
3K