- #1
unscientific
- 1,734
- 13
We know that when a rigid frame, say a rocket undergoes constant proper acceleration, its worldline is hyperbolic. The equation is given by:
[tex] x^2 - c^2t^2 = \left( \frac{c^2}{a_0} \right)^2 [/tex]
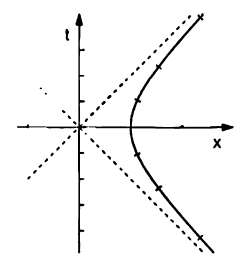
Suppose P is such a worldline and worldine can also be written as:
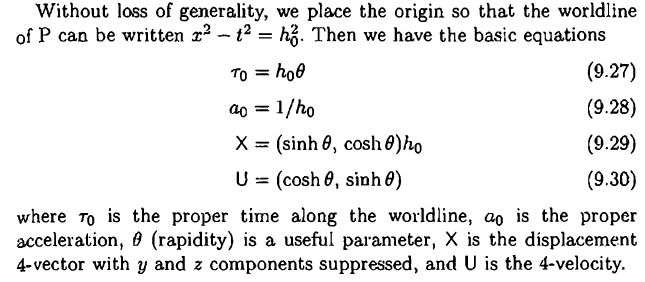
I understand how these are derived up to this point. But it is the reasoning presented below that confuses me.
Things I don't understand:

For completeness, Fig. 9.16 showing the worldlines and lines of simultaneity are shown below:

[tex] x^2 - c^2t^2 = \left( \frac{c^2}{a_0} \right)^2 [/tex]
Suppose P is such a worldline and worldine can also be written as:
I understand how these are derived up to this point. But it is the reasoning presented below that confuses me.
Things I don't understand:
- Why does ## X \cdot U = 0 ## imply that "4-vector from origin to particle is a line of simultaneity for the instantaneous rest frame" ?
- Why do these lines of simultaneity pass through (0,0)? Shouldn't they simply be ##x = \pm ct## based on the first picture?
For completeness, Fig. 9.16 showing the worldlines and lines of simultaneity are shown below: