Rotation of line about rotating axis

[hackhard]

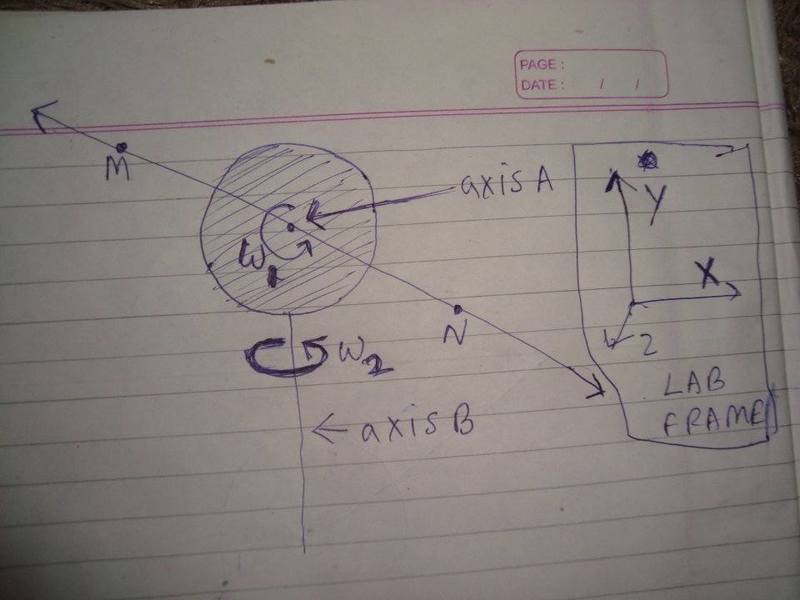
axis A is always normal to plane of the circle and passes thru centre of circle
axis B is always parallel to plane of circle and is always parallel to y- axis of lab frame.
axis B passes thru centre of the circle
the infinitely long line MN always lies on the plane of the circle and passes thru centre of circle
the line MN rotates (in plane of circle) about axis A. with angular velo "w1"
the plane of circle itself rotates about axis B with angular velo "w2"
if w1 is not equal to w2 and
w1 is not equal to w2 / 2 and
w1 /2 is not equal to w2
then -
will the line MN (at some point of time) pass thru every point (coordinates defined wrt lab frame) in 3d space?
(rotations continue forever)

 

[BvU]

If $i * \omega_1 = j * \omega_2$ (with i, j integers) then it's easy to see that MN sweeps through the xy plane at fixed positions. So it's a matter of common dividers. You only excluded i = 2, j = 1.

 

[hackhard]

If $i * \omega_1 = j * \omega_2$ (with i, j integers) then it's easy to see that MN sweeps through the xy plane at fixed positions. So it's a matter of common dividers. You only excluded i = 2, j = 1.

i am adding 3 points to my initial question-
w1 is not an integral multiple of w2
w2 is not an integral multiple of w1
axis B is fixed wrt lab frame

my question remains unchanged -

will the line MN (at some point of time) pass thru every point (coordinates defined wrt lab frame) in 3d space?

 

[BvU]

Moving the goalposts while playing, eh ? Do you know about Lissajous figures ? Your casus is analogous in every possible respect if you think of spherical angular coordinates $\theta$ and $\phi$ instead of x and y.