- #1
blueparukia
- 26
- 0
Been sick for a bit so missed a fair bit of "advanced" maths including locuses, particularly parabolas, but what's worrying me more at the moment is dynamics. So got a moderately difficult question here to help catch me up. I don't really comprehend any of the rules and this question is tricky because it seems I'm going to need trig (albeit basic trig) to find distances and stuff as well as dealing with time.
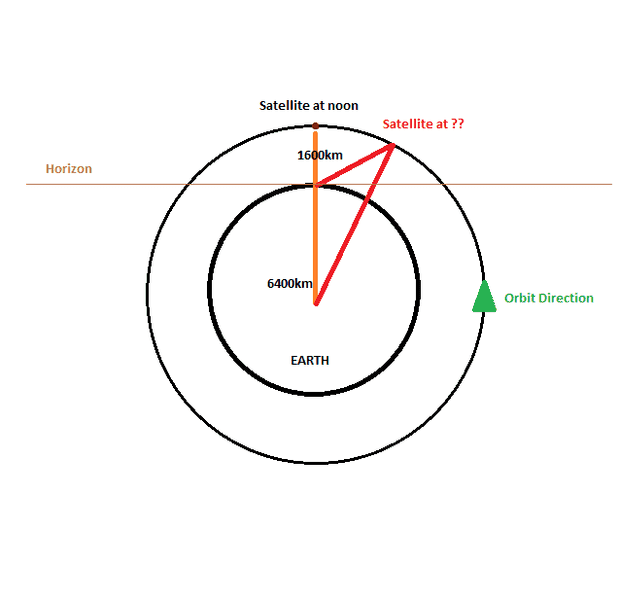
A satellite traveliling in a circular orbit 1600km above the Earth is due to pass over a satellite tracking station at noon. Assume that the satellite takes two hours to make one complete orbit and that the radius of the Earth is 6400km.
If the tracking antenna is aimed 30 degrees above the horizon (an imaginary line, tangent to the Earth and passing through the station), at what time, to the nearest second, will the satellite pass through the beam of the antenna?
w = dx/dt (differential of x/theta n respect to time)
v = wr
T (period) = 2pi/w
Theta = wt
Measure velocity in radians per hour
Homework Statement
A satellite traveliling in a circular orbit 1600km above the Earth is due to pass over a satellite tracking station at noon. Assume that the satellite takes two hours to make one complete orbit and that the radius of the Earth is 6400km.
If the tracking antenna is aimed 30 degrees above the horizon (an imaginary line, tangent to the Earth and passing through the station), at what time, to the nearest second, will the satellite pass through the beam of the antenna?
Homework Equations
w = dx/dt (differential of x/theta n respect to time)
v = wr
T (period) = 2pi/w
Theta = wt
Measure velocity in radians per hour

