- #1
Glenn Rowe
Gold Member
- 24
- 0
I'm trying to work out the Feynman diagrams for scalar-scalar scattering using the Yukawa interaction, as given in Chapter 6 of Lahiri & Pal's A First Book of Quantum Field Theory. The interaction hamiltonian is $$\mathscr{H}_{I}=h:\overline{\psi}\psi\phi:$$ where ##\psi## is a fermion field and ##\phi## is the scalar field. The scattering to be studied is ##BB\rightarrow BB##, where ##B## is a scalar (boson).
If I understand the procedure, we start with an initial state of two bosons (with given momenta) and end up with a final state of two bosons. Thus we must form products of ##\mathscr{H}_{I}## that contain two scalar annihilation operators on the right and two scalar creation operators on the left, which would require a product of 4 time-ordered terms:
$$
\mathscr{T}\left[:\overline{\psi}\psi\phi:_{x_{1}}:\overline{\psi}\psi\phi:_{x_{2}}:\overline{\psi}\psi\phi:_{x_{3}}:\overline{\psi}\psi\phi:_{x_{4}}\right]$$
where the subscripts ##x_1## and so on indicate the spacetime coordinates of each term.
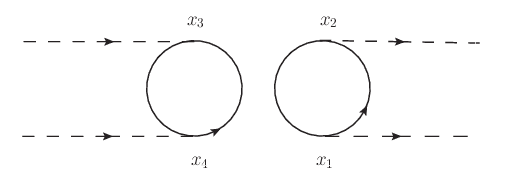
When expanding this using Wick's theorem, we would need to contract all pairs of operators involving ##\overline{\psi}## and ##\psi## (ignoring equal-time contractions). As far as I can tell, this gives rise to 2 types of terms (sorry, but I can't find a way of indicating the underlying brackets for contractions):
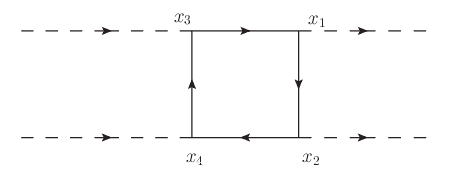
and of (2) is:
A couple of questions...
1. Is that correct?
2. If so, is the first diagram meaningful, seeing as it's disconnected so there doesn't seem to be any way of getting from the incoming particles to the outgoing ones?
Thanks for any help/advice.
If I understand the procedure, we start with an initial state of two bosons (with given momenta) and end up with a final state of two bosons. Thus we must form products of ##\mathscr{H}_{I}## that contain two scalar annihilation operators on the right and two scalar creation operators on the left, which would require a product of 4 time-ordered terms:
$$
\mathscr{T}\left[:\overline{\psi}\psi\phi:_{x_{1}}:\overline{\psi}\psi\phi:_{x_{2}}:\overline{\psi}\psi\phi:_{x_{3}}:\overline{\psi}\psi\phi:_{x_{4}}\right]$$
where the subscripts ##x_1## and so on indicate the spacetime coordinates of each term.
When expanding this using Wick's theorem, we would need to contract all pairs of operators involving ##\overline{\psi}## and ##\psi## (ignoring equal-time contractions). As far as I can tell, this gives rise to 2 types of terms (sorry, but I can't find a way of indicating the underlying brackets for contractions):
- Contract ##\overline{\psi}\left(x_{1}\right)## with ##\psi\left(x_{2}\right)##, ##\psi\left(x_{1}\right)## with ##\overline{\psi}\left(x_{2}\right)##, ##\overline{\psi}\left(x_{3}\right)## with ##\psi\left(x_{4}\right)## and ##\psi\left(x_{3}\right)## with ##\overline{\psi}\left(x_{4}\right)##(and permutations of the spacetime coords)
- Contract ##\overline{\psi}\left(x_{1}\right)## with ##\psi\left(x_{2}\right)##, ##\psi\left(x_{1}\right)## with ##\overline{\psi}\left(x_{3}\right)##, ##\overline{\psi}\left(x_{2}\right)## with ##\psi\left(x_{4}\right)## and ##\psi\left(x_{3}\right)## with ##\overline{\psi}\left(x_{4}\right)##(and permutations of the spacetime coords)
and of (2) is:
A couple of questions...
1. Is that correct?
2. If so, is the first diagram meaningful, seeing as it's disconnected so there doesn't seem to be any way of getting from the incoming particles to the outgoing ones?
Thanks for any help/advice.