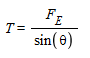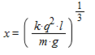Lady M
- 9
- 0
Homework Statement
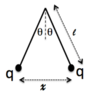
Two identical insulating balls of mass m hang from massless strings of length l and carry identical electric charges, q. you may assume that the angle of separation θ is so small that tanθ ≅sinθ≅θ.
What is the separation distance between the two masses x?
The Attempt at a Solution
I made two attempts at a solution, though it has been so long since I worked a problem like this that I don't know if either attempt is correct (I do know that both methods give different values for x, so at least one is incorrect).
1st using energy conservation:
I believe this method gives the incorrect answer as there is some initial energy between the two particles I have not accounted for, when the potential energy is zero but the energy from the E-field is at its greatest. Because I do not know the diameter of the balls, or their starting position, I assume this method is a bad one?
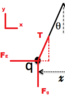
2nd method using statics:
Based off the free body diagram...
thus
so then
where
as such
and finally
Is this correct? Can someone please point me in the right direction?
Attachments
Last edited: