fcoulomb
- 8
- 0
Homework Statement
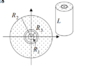
There is a capacitor (llenght ##L##) made of a conductor (cylinder of radius ##R_1##) and a cylindrical surface (radius ##R_2##). It is charged with a potential ##V_0##, then it is isolated.
(There is vacuum between ##R_1## and ##R_2##)
Now we insert a cylindrical conducting shell of thickness ##d##, and inside radius ##R_3##, as in the picture below.1) Find the capacitance before and after the insertion of the shell. Find the value of ##d## such that ##C_{final}=2 C_{initial}## .
The Attempt at a Solution
[/B]
My question is: after the shell is inserted, there is electrostatic induction between the shell and the ##R_1## cylinder, so i can see the problem as two capacitors in series, BUT the total final capacitance would be always less than the initial.
So how I can start?