Shortest distance from A to B to C?

[MariusM]

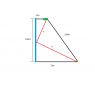
Homework Statement

You are standing on an open field 72,0 m away from a straight river. Your tent is 136 m away from you, while being only 8,0m away from the river (on the same side you are on). Before you go back to your tent, you would like to fill your water bottle in the river. What point on the river should you go to in order for the total trip back to your tent to be the shortest2. The attempt at a solution
I would think that I should find some relations between the rates of change of the hypothenuses of the two triangles I made. This should somehow give me the shortest possible lengths of the hypothenuses combined, but I am not sure how to venture into this problem. Would really appreciate it if someone could set me off in the right direction!

 

[voko]

This problem has one unknown: the vertical coordinate of the watering place. Express the length of the total path as a function of this coordinate, then minimize it.

 

[MariusM]

Ok, thanks.

So call the walking length L. L is split into two legs, leg X and leg Y. Point T is the vertex of X and Y on the river.

X=√(72²+T) and Y=√(8²+(120-T)²)

L=X+Y

L= √(72²+T) + √(8²+(120-T)²)

Taking the derivative of L with respect to T, and letting the derivative of dL/dT = 0 yields the T I want to insert in the orignial function of L. This will give me the correct L? I tried this approach, but it seems awfully long and complex compared to what I would think the real solution is.

 

[HallsofIvy]

The easiest way to do this is to do a "mirror image". Suppose your campsite were on the opposite side of the river, same distance, a mirror image. Clearly, a straight line is the shortest distance between points and, since that line now crosses the river, that is where you should get water. Now use geometry to show that same point gives the shortest distance to your real campsite.

 

[voko]

It does not seem AWFULLY long and complex. I would suggest that instead of the numbers you used some symbols such as a, b, c, it is easier to manipulate those.

I think this is a just a typo, but your expression for X misses the 2 superscript for T.

 

[HallsofIvy]

My suggestion uses NO calculus or derivatives and only linear equations.

 

[MariusM]

Thank you guys very much. I ended up solving it by using the method described by HallsofIvy and got 108m vertically from the point of start.

And yeah, it was just a typo voko :)