Sign convention of internal forces in vertical bars for bending moment

[arestes]

TL;DR

Convention for horizontal beams seems to be void for bending moments when a member is completely vertical.

Hello:
I was looking for a widespread convention (akin to Hibbeler's, Beer's, etc) that deals with the sign convention of a vertical bar for bending moments.
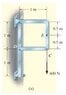
For example, without knowing in advance, how do I draw the bending moment at a cut passing through point E in the figure attached?

Beam sign convention requires that it should be in such a way that it bends with an upward concavity an element containing that point. That doesn't seem to be possible when the member is vertical.Also, now that we're talking about conventions. Are there any conventions in 3D?

 

[Dr.D]

Sign conventions are really unimportant as long as your equations properly reflect whatever convention you choose to use.

 

[arestes]

Sign conventions are really unimportant as long as your equations properly reflect whatever convention you choose to use.

Hi. Yeah. I know. But I was wondering if there is a convention at all.

 

[Lnewqban]

Please, see:
https://en.m.wikipedia.org/wiki/Shear_and_moment_diagram#Convention

Copied from
https://en.m.wikipedia.org/wiki/Bending_moment#Sign_convention

"It is more common to use the convention that a clockwise bending moment to the left of the point under consideration is taken as positive. This then corresponds to the second derivative of a function which, when positive, indicates a curvature that is 'lower at the centre' i.e. sagging. When defining moments and curvatures in this way calculus can be more readily used to find slopes and deflections."

 

[arestes]

Please, see:
https://en.m.wikipedia.org/wiki/Shear_and_moment_diagram#Convention

Copied from
https://en.m.wikipedia.org/wiki/Bending_moment#Sign_convention

"It is more common to use the convention that a clockwise bending moment to the left of the point under consideration is taken as positive. This then corresponds to the second derivative of a function which, when positive, indicates a curvature that is 'lower at the centre' i.e. sagging. When defining moments and curvatures in this way calculus can be more readily used to find slopes and deflections."

Hi. I am aware of this convention (this is what Hibbeler and Beer use) but this fails for vertical members and it's already stated in that wikipedia article: "Since a horizontal member is usually analyzed from left to right and positive in the vertical direction is normally taken to be up, the positive shear convention was chosen to be up from the left, and to make all drawings consistent down from the right".

In short, if the member is vertical, there's no way to bend the element in a "u" shape (sagging). It either bends with curvature to the left or to the right.

 

[Lnewqban]

The convention works if the member is inclined 85° respect to the horizon because there is an up and a down, but it fails if the member is perfectly vertical.
In that case, you create your own convention; the result will be the same, regardless of the adopted new convention.

L-shaped member AC in the posted picture is resisting being deformed in such a way that it would adopt a more straight shape between those two points, if enough force is applied at C.
Therefore, the left side is resisting tension while the right side is resisting compression.
If you tilt your head 45° to the right, you can see the member AC trying to smile at you.