- #1
SweatingBear
- 119
- 0
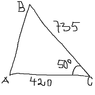
We have a right triangle with sides of length 735 and 420 m where the intermediate angle of aforementioned sides is 50°. The task is simple: Calculate |AB|. Here is a picture:
View attachment 1024
Upon calculating |AB|, we arrive at approximately 565.48 m. My problem is how many significant figures one ought to have in the answer. General practice is to have as many digits as the given data with least amount of significant digits.
But in this case, how many digits can we view the data 420 and 50 respectively to have? Integral values with zeros preceding the decimal point can at times be quite ambiguous. It would not make any sense to say "9 000 000" has seven significant digits since it is given without context.
So, 420 either has two significant digits or three; 50 either has one significant digit or two. 565.48 with three significant digits is 565, two significant digits 570 and one significant digit 600. My intuition tells me to answer 565, but I am really not sure which cases of significant digits to confidently rule out.
View attachment 1024
Upon calculating |AB|, we arrive at approximately 565.48 m. My problem is how many significant figures one ought to have in the answer. General practice is to have as many digits as the given data with least amount of significant digits.
But in this case, how many digits can we view the data 420 and 50 respectively to have? Integral values with zeros preceding the decimal point can at times be quite ambiguous. It would not make any sense to say "9 000 000" has seven significant digits since it is given without context.
So, 420 either has two significant digits or three; 50 either has one significant digit or two. 565.48 with three significant digits is 565, two significant digits 570 and one significant digit 600. My intuition tells me to answer 565, but I am really not sure which cases of significant digits to confidently rule out.