dRic2
Gold Member
- 887
- 225
Imagine to be in 2 dimensions and you have to find the potential generated by 4 point-charges of equal charge located at the four corners of a square.
To do that I think we simply add all the contributions of each single charge:
$$V_i(x, y) = - \frac k {| \mathbf r - \mathbf r_i|}$$
$$ V(x, y) = \sum_i^4 V_i(x,y)$$
where ##\mathbf r_i## is the location of each charge. In particular if I choose the origin of the cartesian coordinates at the center of the square I get (the side of the square was set equal to 2):
##\mathbf r_1 = (-1, -1)##
##\mathbf r_2 = (-1, +1)##
##\mathbf r_3 = (+1, +1)##
##\mathbf r_4 = (+1, -1)##
Now. If I plotted it correctly I get something like this:
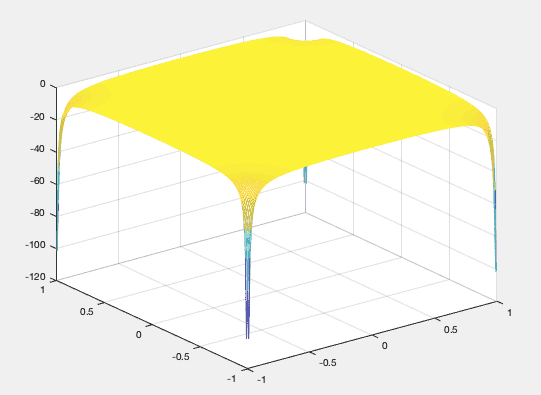
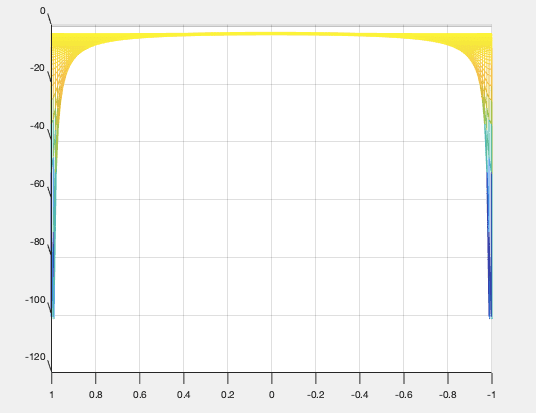
Which clearly has a maximum.
Now consider a circle centered at the origin but smaller than the square so that it contains no charges. Here I can write the Laplace equation:
$$\Delta V = 0$$
$$ + \text{boundary conditions}$$
A particular property of solutions of the Laplace equation is that they can have no local minimum or maximum: al extrema must occur at the boundary. This follows from the property of harmonic functions.
What am I doing wrong here ?
Thanks fro the help.
To do that I think we simply add all the contributions of each single charge:
$$V_i(x, y) = - \frac k {| \mathbf r - \mathbf r_i|}$$
$$ V(x, y) = \sum_i^4 V_i(x,y)$$
where ##\mathbf r_i## is the location of each charge. In particular if I choose the origin of the cartesian coordinates at the center of the square I get (the side of the square was set equal to 2):
##\mathbf r_1 = (-1, -1)##
##\mathbf r_2 = (-1, +1)##
##\mathbf r_3 = (+1, +1)##
##\mathbf r_4 = (+1, -1)##
Now. If I plotted it correctly I get something like this:
Which clearly has a maximum.
Now consider a circle centered at the origin but smaller than the square so that it contains no charges. Here I can write the Laplace equation:
$$\Delta V = 0$$
$$ + \text{boundary conditions}$$
A particular property of solutions of the Laplace equation is that they can have no local minimum or maximum: al extrema must occur at the boundary. This follows from the property of harmonic functions.
What am I doing wrong here ?
Thanks fro the help.
Last edited:
 I missed a ##{1/over 2}## -- twice -- so I ended up with non-zero. Puzzled...
I missed a ##{1/over 2}## -- twice -- so I ended up with non-zero. Puzzled...