Simple Electrical Modeling Question (w/ only C and L)

[Bluestribute]

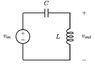
Homework Statement

Find a differential equation that describes the circuit that includes only v_in and v_out as variables.

Homework Equations

C(dv_in - dv_out)/dt = i
v_in - v_out = L(di/dt)

The Attempt at a Solution

So the answer I got was:

C(d²v_out/dt²) + v_out = LC(d²v_in/dt²)

My question is, is it allowable to break up the capacitor derivate like that? After substituting in for i, I got:

v_out = Ld/dt(C(dv_in - dv_out)/dt)

Then I broke up the capacitor into v_in and v_out terms and just rearranged. But I'm not 100% sure if that's legal.

 

[NascentOxygen]

So the answer I got was:

C(d²v_out/dt²) + v_out = LC(d²v_in/dt²)

That first C should be LC.

A rule of the Calculus says that the derivative of a sum equals the sum of the separate derivatives, so your approach is correct.

 

[Bluestribute]

Woopsie, right. LC

Ok sweet, thanks. I just can't remember something we might have glossed over a few years ago . . . and no one recently has said "You can do this to a derivative". They just sort of do it on their own.