dakotapederse
- 1
- 0
Homework Statement
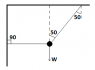
A ball weighing 212-N is shown suspended from a system of cords. What are the tensions in the horizontal and angled cords?
The angles of the cords are 90 and 50
Homework Equations
F=ma