xio
- 11
- 0
[EDIT]: Found the mistake, see the next post.
Evaluate $$\iint_{S}{\rm e}^{x+y}dx\, dy,S=\{(x,y):\left|x\right|+\left|y\right|\leq1\} $$
2. The attempt at a solution
##\left|x\right|+\left|y\right|## is the rhombus with the center at the origin, symmetrical about both axes, so we find the volume at the first quadrant and then multiply by four.
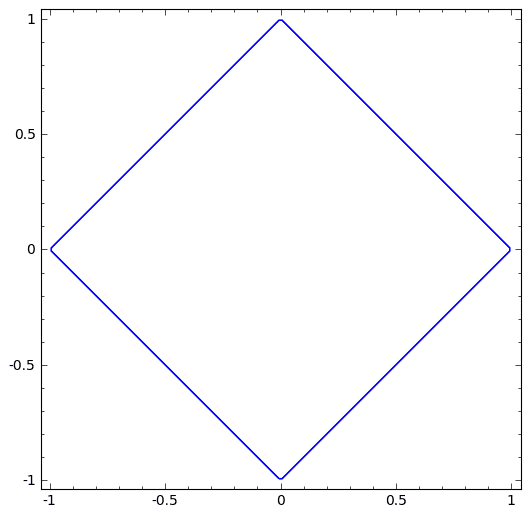
##\varphi(x)=1-x## limits the region of integration and so we have, first integrating over ##y## : $$\iint_{S}{\rm e}^{x+y}dx\, dy=4\int_{0}^{1}\left[\int_{0}^{1-x}{\rm e}^{x}{\rm e}^{y}dy\right]dx=1\neq {\rm e}-{\rm e}^{-1}$$ (I know the correct answer which is ##{\rm e}-{\rm e}^{-1}## )
Apparently so simple, but I just can't see the mistake.
Homework Statement
Evaluate $$\iint_{S}{\rm e}^{x+y}dx\, dy,S=\{(x,y):\left|x\right|+\left|y\right|\leq1\} $$
2. The attempt at a solution
##\left|x\right|+\left|y\right|## is the rhombus with the center at the origin, symmetrical about both axes, so we find the volume at the first quadrant and then multiply by four.
##\varphi(x)=1-x## limits the region of integration and so we have, first integrating over ##y## : $$\iint_{S}{\rm e}^{x+y}dx\, dy=4\int_{0}^{1}\left[\int_{0}^{1-x}{\rm e}^{x}{\rm e}^{y}dy\right]dx=1\neq {\rm e}-{\rm e}^{-1}$$ (I know the correct answer which is ##{\rm e}-{\rm e}^{-1}## )
Apparently so simple, but I just can't see the mistake.
Last edited: