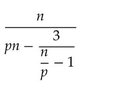SUMMARY
The discussion focuses on simplifying the fractional expression $\frac{n}{p} - 1$. The key transformation presented is that this expression can be rewritten as $\frac{n - p}{p}$. Participants are encouraged to further simplify the denominator, indicating a deeper exploration of algebraic manipulation techniques. The conversation emphasizes the importance of understanding symbolic expressions in Algebra II.
PREREQUISITES
- Understanding of fractional expressions in algebra
- Familiarity with algebraic manipulation techniques
- Knowledge of symbolic representation in mathematics
- Basic skills in simplifying algebraic fractions
NEXT STEPS
- Study techniques for simplifying complex fractions
- Learn about algebraic identities and their applications
- Explore the concept of common denominators in fraction simplification
- Practice solving Algebra II problems involving fractional expressions
USEFUL FOR
Students in Algebra II, educators teaching algebraic concepts, and anyone looking to improve their skills in simplifying mathematical expressions.